DBSCAN clustering

Universidad Central

Maestría en analítica de datos

Métodos estadísticos para analítica de datos.

Docente: Luis Andrés Campos Maldonado.

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import plotly.express as px
from sklearn.preprocessing import StandardScaler, MinMaxScaler
from sklearn.decomposition import PCA
from sklearn.cluster import DBSCAN, AgglomerativeClustering, KMeans
from sklearn.datasets import make_moons
from utils.plots_clustering import *

plt.style.use("ggplot")
plt.rcParams["figure.figsize"] = (15,6)
url_base = "https://raw.githubusercontent.com/lacamposm/Metodos-Estadisticos/main/data/"

Clustering y Limitaciones de K-means y Agglomerative

El clustering es una técnica utilizada para agrupar datos similares. Los algoritmos K-means y Agglomerative Clustering son populares, pero tienen limitaciones con datos de formas no lineales.

• KMeans: Agrupa puntos en función de su distancia a un centroide buscando formar clusters esféricos. En datos con formas complejas K-means tiende a fallar porque intenta forzar grupos esféricos.

• Agglomerative Clustering: Agrupa jerárquicamente los puntos según su cercanía. Aunque más flexible que K-means, también tiene problemas con clusters no convexos o formas irregulares.

X, y = make_moons(n_samples=1000, noise=0.05, random_state=0)
df_moons = pd.DataFrame(X, columns = ["feature_1","feature_2"])
display(df_moons.head())
px.scatter(df_moons, x="feature_1", y="feature_2", title="Make moons - Dataset")

	feature_1	feature_2
0	2.021001	0.490179
1	1.678201	-0.201987
2	-0.282245	0.858785
3	-0.021440	0.176281
4	0.504842	-0.391043

K-means

df_kmeans = df_moons.copy()
scaler = StandardScaler()
scaler_moons = scaler.fit_transform(df_kmeans)
kmeans = KMeans(n_clusters=2)
kmeans.fit(scaler_moons)
df_kmeans["cluster_kmeans"] = kmeans.labels_
df_kmeans["cluster_kmeans"] = df_kmeans["cluster_kmeans"].astype("string")
px.scatter(df_kmeans, x="feature_1", y="feature_2", color="cluster_kmeans", title="Clustering with k-means")

AgglomerativeClustering

df_aglome = df_moons.copy()
aglome = AgglomerativeClustering(n_clusters=2)
aglome.fit(scaler_moons)
df_aglome["cluster_aglome"] = aglome.labels_
df_aglome["cluster_aglome"] = df_aglome["cluster_aglome"].astype("string")
px.scatter(df_aglome, x="feature_1", y="feature_2", color="cluster_aglome", title="Clustering with Agglomerative")

DBSCAN

# Con DBSCAN
df_dbscan = df_moons.copy()
dbscan = DBSCAN(eps=0.2, min_samples=4)
dbscan.fit(df_dbscan)
df_dbscan["cluster_DBSCAN"] = dbscan.labels_
df_dbscan["cluster_DBSCAN"] = df_dbscan["cluster_DBSCAN"].astype("string")

px.scatter(df_dbscan, x="feature_1", y="feature_2", color="cluster_DBSCAN", title="Clustering with DBSCAN").show()

# ***Note el único método que segmentó de manera adecuada fue DBSCAN.***

# Cuando se aplican algoritmos de clustering, por lo general no existe una "verdad" básica con la cual comparar los resultados.
# Hay métricas de puntuación para el clustering como el coeficiente de silueta. Este coeficiente calcula la compacidad de un clúster, 
# donde un valor más alto es mejor, con una puntuación perfecta de 1. Si bien los clústeres compactos son buenos, la compacidad no 
# trabaja bien en formas complejas formas.

algoritms = [kmeans, aglome, dbscan]

for algoritm in algoritms:
    clusters = algoritm.fit_predict(scaler_moons)
    score = silhouette_score(scaler_moons, clusters)
    print(f"Algoritmo: {algoritm} ---> silhouette_score: {score: .3f}")

Algoritmo: KMeans(n_clusters=2) ---> silhouette_score:  0.499
Algoritmo: AgglomerativeClustering() ---> silhouette_score:  0.457
Algoritmo: DBSCAN(eps=0.2, min_samples=4) ---> silhouette_score:  0.392

\(K\)-means obtiene la puntuación de silueta más alta, aunque se prefiere el resultado obtenido por DBSCAN.

DBSCAN (Density-based spatial clustering of applications with noise)

DBSCAN (“clustering con ruido basado en la densidad”) es un algoritmo de clustering que busca la identificación de regiones “pobladas”, es decir donde muchos registros están muy juntos, estas regiones se conocen como regiones densas en el espacio de datos.

La idea básica detrás de este enfoque de clustering se deriva de un método humano de agrupamiento intuitivo. Es decir, el cerebro humano puede identificar clusters observando los puntos que están cerca y además dejando sin ninguna asignación a registros que están aíslados (ruído). Así, los clusters son regiones densas en el espacio de datos, separadas por regiones de menor densidad de puntos. El algoritmo DBSCAN se basa en esta noción intuitiva de “clusters” y “ruido”. La idea clave es que para cada punto de un cluster, la vecindad tiene que contener al menos un número mínimo de puntos.

Los principales beneficios de DBSCAN son que no requiere que el usuario establezca el número de clusters a priori, puede capturar clusters de formas complejas y puede identificar puntos que no forman parte de ningún cluster. El algoritmo DBSCAN es algo más lento que el clustering aglomerativo y que \(K\)-means. Este algoritmo puede utilizarse para identificar clusters de cualquier forma en un Dataset que contenga ruido y valores atípicos.

Ideas del método.

La idea detrás de DBSCAN es que los clusters forman regiones densas de datos, separadas por regiones que están relativamente vacías. Los puntos que están dentro de una región densa se denominan core points (core points). Hay dos parámetros en DBSCAN: min_samples y eps. Si hay al menos min_samples puntos dentro de una distancia eps (\(ϵ\)-vecindad), ese punto se clasifica como un core point. Core points que están más cerca entre sí que la distancia eps el algoritmo DBSCAN los coloca en el mismo cluster.

El algoritmo funciona eligiendo un punto arbitrario para comenzar. Luego encuentra todos los puntos con distancia menor o igual a la dada en eps (definición de \(ϵ\)-vecindad). Si hay menos de min_samples puntos dentro de la distancia eps del punto de partida, este punto se etiqueta como ruido, lo que significa que no pertenece a ningún cluster (por ahora). Si hay más de min_samples puntos dentro de una distancia eps, el punto se etiqueta como core point y se le asigna una nueva etiqueta de cluster. Luego, se visitan todos los vecinos (“viaja” por la \(ϵ\)-vecindad) del punto, a estos puntos se les asigna la nueva etiqueta de cluster que se acaba de crear. Si son core points, sus vecinos son visitados a su vez, y así sucesivamente. El cluster crece hasta que no hay más core points a una distancia eps del cluster. Después se elige otro punto que aún no ha sido visitado, y se sigue el mismo procedimiento anterior.

ALGORITMO DBSCAN

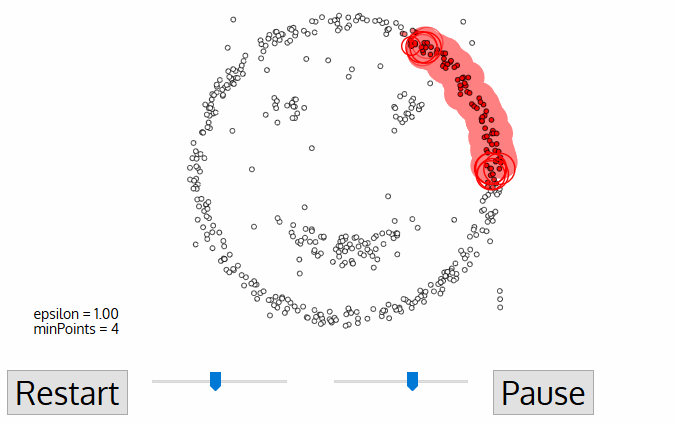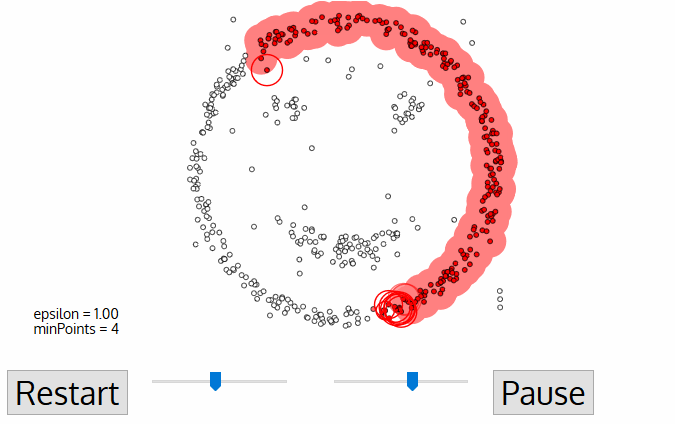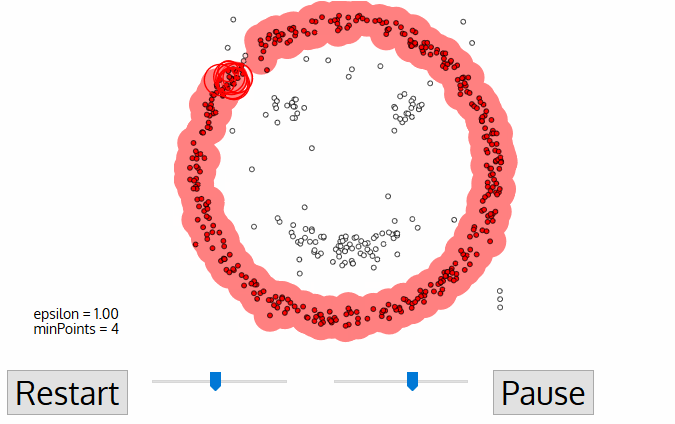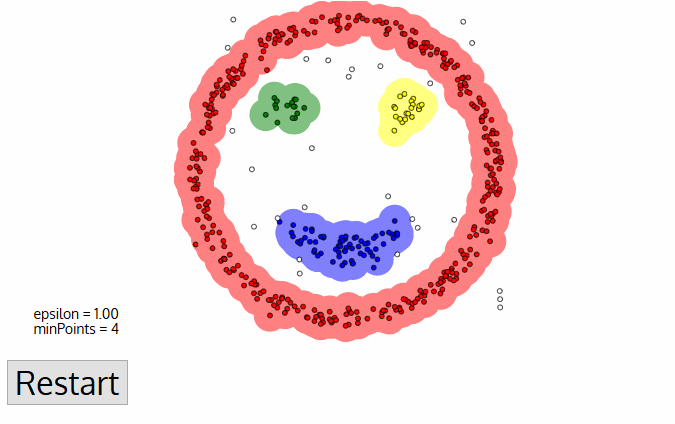
Algoritmo DBSCAN

Vamos a definir tres conceptos:

• Core point: Una observación que tiene en su \(ϵ\)-vecindad un número de observaciones vecinas igual o mayor que min_sample.

• Boder point: Una observación que no satisface el número mínimo de observaciones vecinas para ser core point, pero pertenece a la \(ϵ\)-vecindad de otra observación que si es core point.

• Noise u outlier: Una observación que no es core point ni border point.

Basados en las tres categorías anteriores se pueden definir tres niveles de conectividad entre observaciones:

• Directamente alcanzable (direct density reachable): Una observación \(B\) es directamente alcanzable desde otra observación \(A\) si \(B\) forma parte de la \(ϵ\)-vecindad de \(A\) y \(A\) es un core point. Por definición, las observaciones solo pueden ser directamente alcanzables desde un core point.

• Alcanzable (density reachable): Una observación \(A\) es alcanzable desde otra observación \(B\) si existe una secuencia de core points que van desde \(B\) a \(A\).

• Densamente conectadas (density conected): Dos observaciones \(B\) y \(C\) están densamente conectadas si existe una observación \(A\) que es un core point, tal que \(B\) y \(C\) son alcanzables desde \(A\).

Tomado de wikipedía

La imagen anterior muestra las conexiones existentes entre un conjunto de observaciones con min_samples=4. La observación \(A\) y el resto de observaciones marcadas con rojo son core points, ya que todas ellas contienen al menos 4 observaciones vecinas (incluyéndose a ellas mismas) en su \(\epsilon\)-vecindad. Como todas son alcanzables entre ellas, forman un cluster. Las observaciones \(B\) y \(C\) no son core points, pero son densamente alcanzables desde \(A\) y densamente conectados con A, y por lo tanto pertenecen al mismo clúster. La observación \(N\) no es ni core point ni es directamente alcanzable, por lo tanto se considera como noise (ruido)

Algoritmo.

1. Para cada observación \(x_i\) calcular la distancia entre ella y el resto de observaciones. Si en su \(ϵ\)-vecindad hay un número de observaciones mayor o igual a min_sample marcar la observación como core point, de lo contrario marcarla como visitada.

2. Para cada observación \(x_i\) marcada como core point, si todavía no ha sido asignada a ningún cluster, crear uno nuevo y asignarla a él. Encontrar recursivamente todas las observaciones densamente conectadas a ella y asignarlas al mismo cluster.

3. Iterar el mismo proceso para todas las observaciones que no hayan sido visitadas.

4. Aquellas observaciones que tras haber sido visitadas no pertenecen a ningún cluster se marcan como outliers.

NOTA: Como resultado, todo cluster cumple dos propiedades:

1. Todos los puntos que forman parte de un mismo cluster están densamente conectados entre ellos.

2. Si una observación \(A\) es densamente alcanzable desde cualquier otra observación de un cluster, entonces \(A\) también pertenece al cluster.

Selección de parámetros.

Como ocurre en muchas otras técnicas estadísticas, en DBSCAN no existe una forma única y exacta de encontrar el valor adecuado de epsilon (eps) y min_samples. A modo orientativo se pueden seguir las siguientes premisas:

• min_samples: Cuanto mayor sea el tamaño del Dataset, mayor debe ser el valor mínimo de observaciones vecinas. En el libro de la referencia 1, recomiendan no bajar nunca de 3. Si los datos contienen niveles altos de ruido, aumentar min_samples favorecerá la creación de clusters significativos menos influenciados por outliers.

• eps: Una buena forma de escoger este valor consiste en calcular las distancias al \(k\)-ésimo vecino más cercano (donde \(k\) corresponde a min_samples). Luego, estas k-ésimas distancias se trazan en orden ascendente. El objetivo es determinar la “rodilla”, que corresponde al parámetro eps óptimo. Una rodilla corresponde a un umbral donde se produce un cambio brusco a lo largo de la curva de las k-ésimas distancias. Si el valor de eps escogido es muy pequeño, una proporción alta de las observaciones no se asignarán a ningún clúster, mientras que si el valor es demasiado grande, la mayoría de las observaciones se agruparán en un único clúster.

• Distancia k de la curva: Estudiar las distancias promedio entre las \(k\) (min_samples) observaciones más próximas. Al representar estas distancias en función de eps, el punto de inflexión de la curva suele ser un valor óptimo. Si el valor de eps escogido es muy pequeño, una proporción alta de las observaciones no se asignarán a ningún cluster, por el contrario, si el valor es demasiado grande, la mayoría de observaciones se agruparán en un único cluster.

Ventajas de DBSCAN.

• A diferencia de \(K\)-means, DBSCAN no requiere que el usuario especifique el número de clusters a generar.

• DBSCAN es independiente de la forma que tengan los clusters, no tienen por qué ser circulares o convexos.

• DBSCAN puede identificar outliers, por lo que los clusters generados no son influenciados por ellos.

Desventajas de DBSCAN.

• No es un método totalmente determinístico: los border points que son alcanzables desde más de un cluster pueden asignarse a uno u otro dependiendo del orden en el que se procesen los datos.

• No genera buenos resultados cuando la densidad de los grupos es muy distinta, ya que no es posible encontrar los parámetros eps y min_samples que sirvan para todos a la vez.

Ejemplo 1.

Vamos a hacer uso de sklearn.cluster.DBSCAN para trabajar con el algoritmo.

df_usarrests = pd.read_csv(url_base + "USArrests.csv", index_col=0)
df_usarrests.head()

	Murder	Assault	UrbanPop	Rape
Alabama	13.2	236	58	21.2
Alaska	10.0	263	48	44.5
Arizona	8.1	294	80	31.0
Arkansas	8.8	190	50	19.5
California	9.0	276	91	40.6

# Escalamos la información.
scaler = StandardScaler()
#
df_scaler = pd.DataFrame(scaler.fit_transform(df_usarrests), columns=df_usarrests.columns, index=df_usarrests.index)
df_scaler.head(6)

	Murder	Assault	UrbanPop	Rape
Alabama	1.255179	0.790787	-0.526195	-0.003451
Alaska	0.513019	1.118060	-1.224067	2.509424
Arizona	0.072361	1.493817	1.009122	1.053466
Arkansas	0.234708	0.233212	-1.084492	-0.186794
California	0.281093	1.275635	1.776781	2.088814
Colorado	0.025976	0.402909	0.869548	1.883901

knn_plot_dbscan(df_scaler, min_samples=2)

# Creamos una instancia de DBSCAN
clustering = DBSCAN(eps=1.349, min_samples=8)
clustering.fit(df_scaler)
np.unique(clustering.labels_, return_counts=True)

(array([-1,  0,  1,  2]), array([ 5,  8, 32,  5]))

# Ajustamos un PCA
pca = PCA(n_components=0.90)
pca.fit(df_scaler)
pca_array = pca.transform(df_scaler)

# Plot con 2 clusters.
cluster_biplot(pca, df_usarrests, clustering.labels_, size_text=5)

# Comparando clusters.
df_cluster = df_usarrests.copy()
df_cluster["cluster"] = clustering.labels_
df_cluster.head()

	Murder	Assault	UrbanPop	Rape	cluster
Alabama	13.2	236	58	21.2	0
Alaska	10.0	263	48	44.5	-1
Arizona	8.1	294	80	31.0	2
Arkansas	8.8	190	50	19.5	0
California	9.0	276	91	40.6	-1

df_cluster_plot = df_cluster.query("cluster !=-1")
df_cluster_plot["cluster"] = df_cluster_plot["cluster"].astype("category")

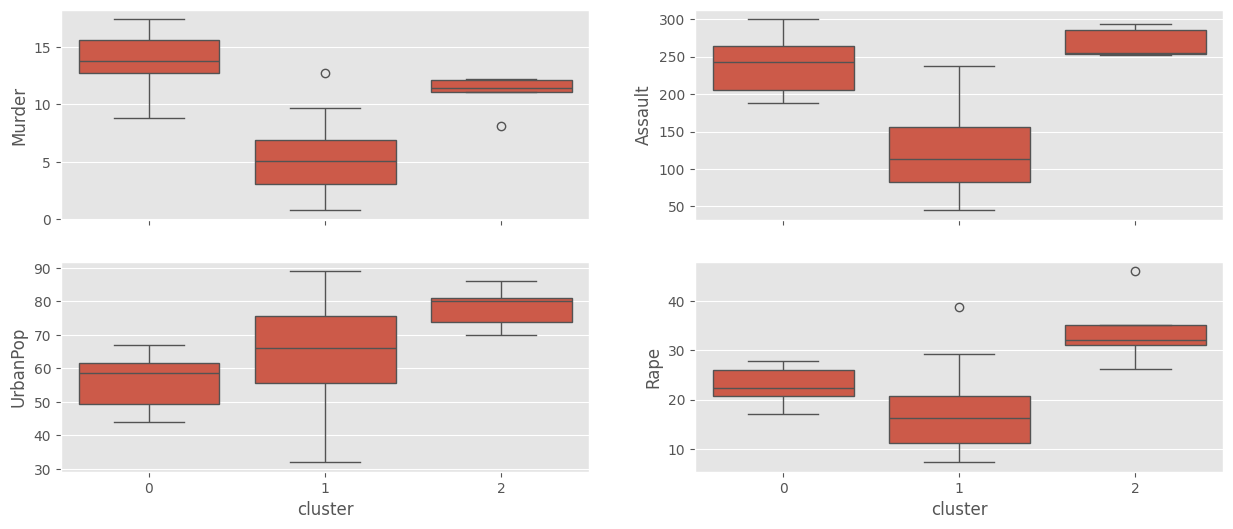
# Box-plots
fig, axes = plt.subplots(2,2, sharex=True)
#
sns.boxplot(data=df_cluster_plot, x = "cluster", y = "Murder", ax = axes[0,0])
sns.boxplot(data=df_cluster_plot, x = "cluster", y = "Assault", ax = axes[0,1])
sns.boxplot(data=df_cluster_plot, x = "cluster", y = "UrbanPop", ax = axes[1,0])
sns.boxplot(data=df_cluster_plot, x = "cluster", y = "Rape", ax = axes[1,1])
plt.show()

OTRO ESCALADOR.

# Escalamos la información.
scaler_min_max = MinMaxScaler()
min_max_transform = scaler_min_max.fit_transform(df_usarrests)
##
df1 = pd.DataFrame(min_max_transform, columns=df_usarrests.columns, index = df_usarrests.index)
df1.head(6)

	Murder	Assault	UrbanPop	Rape
Alabama	0.746988	0.654110	0.440678	0.359173
Alaska	0.554217	0.746575	0.271186	0.961240
Arizona	0.439759	0.852740	0.813559	0.612403
Arkansas	0.481928	0.496575	0.305085	0.315245
California	0.493976	0.791096	1.000000	0.860465
Colorado	0.427711	0.544521	0.779661	0.811370

knn_plot_dbscan(df1, min_samples=2)

clustering = DBSCAN(eps=0.35, min_samples=8)
clustering.fit(df1)
np.unique(clustering.labels_, return_counts=True)

(array([-1,  0,  1,  2]), array([ 4,  8, 32,  6]))

clustering.labels_

array([ 0, -1,  2,  0, -1,  1,  1,  1, -1,  0,  1,  1,  2,  1,  1,  1,  1,
        0,  1,  0,  1,  2,  1,  0,  1,  1,  1,  2,  1,  1,  2,  2, -1,  1,
        1,  1,  1,  1,  1,  0,  1,  0,  1,  1,  1,  1,  1,  1,  1,  1])

pca = PCA(n_components=0.90)
pca_transform_min_max = pca.fit_transform(df1)
pd.DataFrame(pca_transform_min_max).head()

	0	1	2
0	0.293082	-0.273177	-0.098603
1	0.497299	-0.225498	0.501542
2	0.460302	0.201380	0.003031
3	-0.006003	-0.275698	0.028729
4	0.612016	0.409985	0.143261

knn_plot_dbscan(pca_transform_min_max, min_samples=2)

clustering = DBSCAN(eps=0.258, min_samples=6)
clustering.fit(pca_transform_min_max)
np.unique(clustering.labels_, return_counts=True)

(array([-1,  0,  1,  2]), array([ 8,  6, 30,  6]))

Ejemplo 2.

Vamos a considerar la siguiente data de clientes, la idea será realizar una segmentación de esta información

# Clientes 
path = "clientes_clustering.csv"
clientes = pd.read_csv(url_base + path, index_col=0)
clientes

	Genre	Age	Annual Income (k$)	Spending Score (1-100)
CustomerID
1	Male	19	15	39
2	Male	21	15	81
3	Female	20	16	6
4	Female	23	16	77
5	Female	31	17	40
...	...	...	...	...
196	Female	35	120	79
197	Female	45	126	28
198	Male	32	126	74
199	Male	32	137	18
200	Male	30	137	83

200 rows × 4 columns

px.scatter(clientes, x="Annual Income (k$)", y="Spending Score (1-100)", color="Genre").show()
px.scatter(clientes, x="Age", y="Spending Score (1-100)", color="Genre").show()

df2 = clientes.copy()
df2 = df2.iloc[:,1:]
df2.head()

	Age	Annual Income (k$)	Spending Score (1-100)
CustomerID
1	19	15	39
2	21	15	81
3	20	16	6
4	23	16	77
5	31	17	40

scaler = StandardScaler()

df2_dbscan = pd.DataFrame(scaler.fit_transform(clientes.select_dtypes(np.number)), columns=df2.columns)
df2_dbscan

	Age	Annual Income (k$)	Spending Score (1-100)
0	-1.424569	-1.738999	-0.434801
1	-1.281035	-1.738999	1.195704
2	-1.352802	-1.700830	-1.715913
3	-1.137502	-1.700830	1.040418
4	-0.563369	-1.662660	-0.395980
...	...	...	...
195	-0.276302	2.268791	1.118061
196	0.441365	2.497807	-0.861839
197	-0.491602	2.497807	0.923953
198	-0.491602	2.917671	-1.250054
199	-0.635135	2.917671	1.273347

200 rows × 3 columns

knn_plot_dbscan(df2_dbscan, min_samples=2)

clustering2 = DBSCAN(eps=0.606, min_samples=6)
clustering2.fit(df2_dbscan)
np.unique(clustering2.labels_, return_counts=True)

(array([-1,  0,  1,  2,  3,  4]), array([ 33, 106,   5,   4,  34,  18]))

pca = PCA(n_components=0.9)
pca.fit(df2_dbscan)
cluster_biplot(pca, clientes.drop(columns=["Genre"]), clustering2.labels_, size_text=5)

Referencias:

1. Multivariate Analysis I. Kassambara A. Disponible en: http://www.sthda.com/english/

2. Selecting the number of clusters with silhouette analysis on KMeans clustering by sklearn