Algunas Implementaciones de Gradient-Boosting.#
Universidad Central#
Maestría en analítica de datos#
Métodos estadísticos para analítica de datos.#
Docente: Luis Andrés Campos Maldonado.#
# Librerias para Colab
# !pip install xgboost catboost lightgbm sweetviz
# Paquetes a usar.
import warnings
warnings.filterwarnings("ignore")
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import plotly.express as px
from sweetviz import analyze
from sklearn.compose import ColumnTransformer
from sklearn.preprocessing import OneHotEncoder
from sklearn.model_selection import RandomizedSearchCV, train_test_split, cross_validate
from sklearn.pipeline import Pipeline
from xgboost.sklearn import XGBRegressor
from lightgbm import LGBMRegressor
from catboost import CatBoostRegressor
plt.rcParams["figure.figsize"] = (15,6)
pd.set_option("display.max_columns", None)
url_base = "https://raw.githubusercontent.com/lacamposm/Metodos-Estadisticos/main/data/"
Introducción a XGBoost, LightGBM y CatBoost#
Los modelos de Gradient Boosting son algoritmos de aprendizaje supervisado que combinan múltiples modelos base (habitualmente árboles de decisión) para construir un modelo predictivo más fuerte. Este enfoque se basa en entrenar modelos de manera secuencial, donde cada modelo corrige los errores cometidos por los modelos anteriores.
A lo largo de los años, han surgido implementaciones optimizadas de Gradient Boosting que mejoran la velocidad, la precisión y la facilidad de uso. Entre las más populares se encuentran:
XGBoost (Extreme Gradient Boosting): Reconocido por su alto rendimiento y flexibilidad.
LightGBM (Light Gradient Boosting Machine): Diseñado para ser rápido y eficiente en el uso de memoria.
CatBoost (Categorical Boosting): Especializado en el manejo de datos categóricos.
Regularización en XGBoost, LightGBM y CatBoost#
La regularización es una técnica fundamental en aprendizaje automático para prevenir el sobreajuste (overfitting), que ocurre cuando un modelo se ajusta demasiado a los datos de entrenamiento y pierde la capacidad de generalizar sobre nuevos datos. Los algoritmos de Gradient Boosting, como XGBoost, LightGBM y CatBoost, integran diversas formas de regularización para equilibrar la complejidad del modelo y su capacidad predictiva.
¿Qué regula la regularización?#
En Gradient Boosting, la regularización actúa directamente sobre los árboles base y sus contribuciones al modelo final. Específicamente:
Los pesos de las hojas de los árboles (\(w_j\)):
Estos pesos determinan el valor predicho por cada hoja.
Penalizaciones como \(L_{1}\) y \(L_{2}\) ajustan estos pesos para reducir su magnitud o eliminarlos por completo, evitando ajustes excesivos.
La estructura de los árboles (profundidad y número de hojas):
Al limitar la expansión de los árboles, la regularización previene que los árboles aprendan patrones específicos de los datos de entrenamiento que no generalizan bien.
El impacto de cada árbol base \(f_m(x)\) en el ensemble final:
A través del coeficiente de aprendizaje (\(\nu\)), se escala la contribución de cada árbol, asegurando actualizaciones más progresivas y menos propensas al sobreajuste.
Conceptos clave de regularización#
En el contexto del boosting, la regularización se introduce para controlar la complejidad de los árboles y el impacto de cada modelo base en el ensemble final. Las formas más comunes de regularización incluyen:
Penalización L1 (Lasso):
Introduce un término de penalización proporcional a la suma de los valores absolutos de los pesos de las hojas:\[ \Omega_L = \alpha \sum_{j=1}^T |w_j|\]Esto fomenta que algunos pesos sean exactamente 0, eliminando hojas innecesarias y promoviendo modelos más simples.
Penalización L2 (Ridge):
Agrega un término de penalización proporcional al cuadrado de los pesos de las hojas:\[\Omega_R = \frac{\lambda}{2} \sum_{j=1}^T w_j^2\]Esto reduce la magnitud de los pesos, suavizando las predicciones y haciendo el modelo más conservador.
XGBoost (Extreme Gradient Boosting)#
XGBoost es una implementación avanzada de Gradient Boosting, conocida por su alto rendimiento, precisión y flexibilidad. Es ampliamente utilizada en competiciones de ciencia de datos y problemas del mundo real debido a su capacidad para manejar datos grandes y complejos.
Características principales:#
Regularización avanzada:
XGBoost utiliza penalizaciones para controlar la complejidad de los árboles y evitar el sobreajuste, promoviendo modelos más simples y generalizables.
Optimización eficiente:
Implementa cálculos paralelos, lo que acelera el entrenamiento en comparación con otras herramientas.
Control de la estructura de los árboles:
Limita el crecimiento de los árboles, asegurando que no sean excesivamente complejos y puedan generalizar mejor.
Ventajas:#
Precisión: Ofrece resultados muy exactos gracias a sus técnicas avanzadas de regularización.
Escalabilidad: Es capaz de manejar grandes conjuntos de datos de manera eficiente.
Flexibilidad: Permite personalizar la función de pérdida y trabajar con diferentes tipos de datos.
Limitaciones:#
Puede ser más lento que otras herramientas en conjuntos de datos extremadamente grandes.
Requiere un ajuste cuidadoso de hiperparámetros para obtener su máximo potencial.
Cuándo usar XGBoost:#
Para problemas que requieren alta precisión.
En tareas donde el control y ajuste de los parámetros son cruciales.
En competiciones de ciencia de datos o proyectos complejos.
Hiperparámetros de XGBoost y consejos de su uso#
Configurar los hiperparámetros de XGBoost de manera adecuada es crucial para obtener un modelo óptimo. Aunque el ajuste depende del problema específico, existen valores iniciales recomendados y estrategias comunes para lograr un buen desempeño.
Hiperparámetros principales#
learning_rate(Coeficiente de aprendizaje):Controla el impacto de cada árbol base en el modelo final.
Recomendación: Usar un valor pequeño como
0.01o0.1y aumentar el número de árboles (n_estimators).Consejo: Si se requiere mayor velocidad de entrenamiento, valores más altos como
0.2o0.3pueden ser utilizados, pero existe mayor riesgo de sobreajuste.
max_depth(Profundidad máxima):Determina la profundidad máxima de los árboles base, controlando la complejidad del modelo.
Recomendación:
Usar valores pequeños (
3a6) para conjuntos de datos pequeños o con ruido.Valores mayores (
6a10) pueden funcionar mejor para datos grandes, aunque aumentan el riesgo de sobreajuste.
n_estimators(Número de árboles):Define cuántos árboles base se ajustarán secuencialmente.
Recomendación:
Comenzar con un valor alto (
100a500) si se usa unlearning_ratebajo.Utilizar validación cruzada para determinar el número óptimo.
subsample(Tasa de muestreo):Especifica la fracción de datos utilizados para construir cada árbol.
Recomendación:
Valores entre
0.7y0.9suelen funcionar bien.Reducir este valor ayuda a prevenir el sobreajuste.
colsample_bytree(Columnas por árbol):Fracción de características consideradas al construir cada árbol.
Recomendación:
Valores entre
0.5y0.8equilibran precisión y tiempo de entrenamiento.
reg_alpha(Regularización L1):Controla la penalización L1, promoviendo modelos más esparsos.
Recomendación:
Comenzar con valores bajos (
0a1) y aumentar si hay sobreajuste.
reg_lambda(Regularización L2):Controla la penalización L2, reduciendo la magnitud de los pesos de las hojas.
Recomendación:
Valores moderados (
1a10) suelen ser efectivos.
gamma(Penalización por división):Requiere que las divisiones superen un umbral mínimo de ganancia.
Recomendación:
Valores iniciales de
0(sin penalización) y aumentar si se detecta sobreajuste.
Estrategia para el ajuste de hiperparámetros#
Comenzar con valores predeterminados:
XGBoost tiene configuraciones predeterminadas robustas para muchos problemas.
Ajustar primero
learning_rate,max_depth, yn_estimators.
Validación cruzada:
Utilizar validación cruzada para evaluar el rendimiento en diferentes configuraciones de hiperparámetros.
Grid Search o Random Search:
Implementar búsquedas sistemáticas (
GridSearchCV) o aleatorias (RandomizedSearchCV) para explorar combinaciones de hiperparámetros.
Experimentar con datos grandes:
Reducir
subsampleycolsample_bytreepara acelerar el entrenamiento y evitar sobreajuste.
Ejemplo 1.#
# Importamos el DataSet.
df = pd.read_csv(url_base + "kc_house_data.csv",)
df.head()
| id | date | price | bedrooms | bathrooms | sqft_living | sqft_lot | floors | waterfront | view | condition | grade | sqft_above | sqft_basement | yr_built | yr_renovated | zipcode | lat | long | sqft_living15 | sqft_lot15 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 7129300520 | 20141013T000000 | 221900.0 | 3 | 1.00 | 1180 | 5650 | 1.0 | 0 | 0 | 3 | 7 | 1180 | 0 | 1955 | 0 | 98178 | 47.5112 | -122.257 | 1340 | 5650 |
| 1 | 6414100192 | 20141209T000000 | 538000.0 | 3 | 2.25 | 2570 | 7242 | 2.0 | 0 | 0 | 3 | 7 | 2170 | 400 | 1951 | 1991 | 98125 | 47.7210 | -122.319 | 1690 | 7639 |
| 2 | 5631500400 | 20150225T000000 | 180000.0 | 2 | 1.00 | 770 | 10000 | 1.0 | 0 | 0 | 3 | 6 | 770 | 0 | 1933 | 0 | 98028 | 47.7379 | -122.233 | 2720 | 8062 |
| 3 | 2487200875 | 20141209T000000 | 604000.0 | 4 | 3.00 | 1960 | 5000 | 1.0 | 0 | 0 | 5 | 7 | 1050 | 910 | 1965 | 0 | 98136 | 47.5208 | -122.393 | 1360 | 5000 |
| 4 | 1954400510 | 20150218T000000 | 510000.0 | 3 | 2.00 | 1680 | 8080 | 1.0 | 0 | 0 | 3 | 8 | 1680 | 0 | 1987 | 0 | 98074 | 47.6168 | -122.045 | 1800 | 7503 |
df_temp = df.copy()
df_temp = df_temp.drop(columns=["id", "sqft_living15", "sqft_lot15", "date"])
df_temp["renovated"] = df_temp["yr_renovated"] > 0
df_temp.drop(columns=["yr_renovated"], inplace=True)
df_temp[["waterfront", "view", "renovated", "zipcode"]] = df_temp[["waterfront", "view", "renovated", "zipcode"]].astype("category")
report = analyze(df_temp, target_feat="price")
report.show_notebook()
del df_temp
plt.style.use("ggplot")
# Prepocesamiento de la Data.
df_to_model = df.copy()
df_to_model = df_to_model.drop(columns=["id", "sqft_living15", "sqft_lot15", "date"])
df_to_model["renovated"] = df_to_model["yr_renovated"] > 0
df_to_model.drop(columns=["yr_renovated"], inplace=True)
df_to_model.drop_duplicates(inplace=True)
# Definimos variable objetivo y predictores. Tomamos además set de train y set de test.
X = df_to_model.drop(columns=["price"])
y = df_to_model["price"]
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=123)
features_categoric = ["waterfront", "view", "renovated", "zipcode"]
features_numerical = [col for col in X.columns if col not in features_categoric]
preprocessor = ColumnTransformer(
transformers=[
("cat", OneHotEncoder(), features_categoric),
("num", "passthrough", features_numerical)
]
)
Modelo con XGBoost#
xgb_regressor_ = XGBRegressor()
xgb_regressor_.fit(X_train, y_train)
print(f"Train set score: {xgb_regressor_.score(X_train, y_train):.4f}")
print(f"Test set score: {xgb_regressor_.score(X_test, y_test):.4f}")
Train set score: 0.9758
Test set score: 0.8693
xgb_regressor1 = XGBRegressor(
objective="reg:squarederror",
max_depth=3,
n_estimators=2000,
learning_rate=0.0075,
reg_alpha=300,
reg_lambda=250,
max_leaves=150,
subsample=0.8,
)
pipeline = Pipeline(steps=[
("preprocessor", preprocessor),
("model", xgb_regressor1)
])
pipeline.fit(X_train, y_train)
print(f"R2 en Train: {pipeline.score(X_train, y_train):.4f}")
print(f"R2 en Test: {pipeline.score(X_test, y_test):.4f}")
cv_xgb = cross_validate(
pipeline,
X_train,
y_train,
cv=5,
scoring="r2",
return_train_score=True
)
train_lr, test_lr = cv_xgb["train_score"], cv_xgb["test_score"]
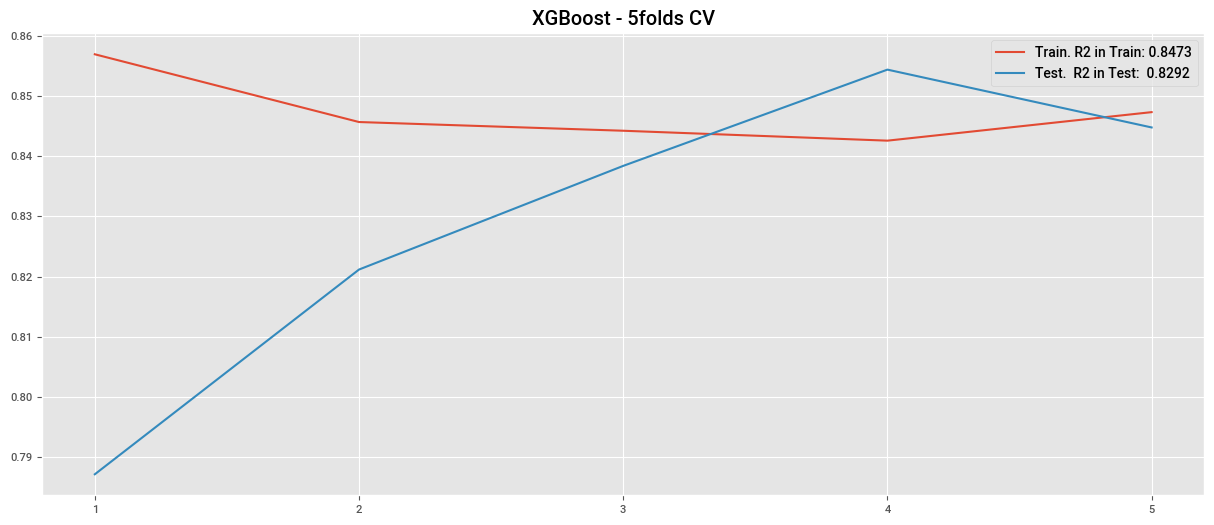
plt.plot(cv_xgb["train_score"], label=f"Train. R2 in Train: {train_lr.mean():.4f}")
plt.plot(cv_xgb["test_score"], label=f"Test. R2 in Test: {test_lr.mean():.4f}")
plt.title("XGBoost - 5folds CV")
plt.xticks(np.arange(0,5), np.arange(1,6))
plt.legend()
plt.show()
R2 en Train: 0.8524
R2 en Test: 0.8425
cv_xgb = cross_validate(
pipeline,
X_train,
y_train,
cv=5,
scoring="neg_mean_absolute_error",
return_train_score=True
)
train_lr, test_lr = cv_xgb["train_score"], cv_xgb["test_score"]
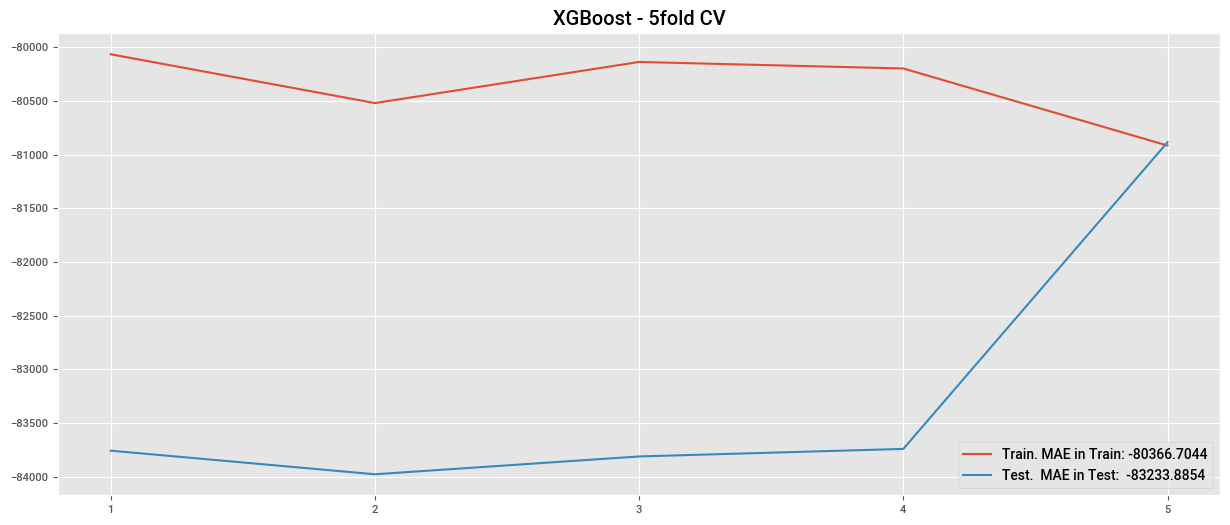
plt.plot(cv_xgb["train_score"], label=f"Train. MAE in Train: {train_lr.mean():.4f}")
plt.plot(cv_xgb["test_score"], label=f"Test. MAE in Test: {test_lr.mean():.4f}")
plt.title("XGBoost - 5fold CV")
plt.legend()
plt.xticks(np.arange(0,5), np.arange(1,6))
plt.show()
df_results_train = pd.DataFrame(
{
"true_value": y_train,
"predicted_value": pipeline.predict(X_train)
}
)
df_results_train["diff"] = abs(df_results_train["true_value"] - df_results_train["predicted_value"])
display(df_results_train.sort_values("diff", ascending=False).head(20))
df_results_test = pd.DataFrame(
{
"true_value": y_test,
"predicted_value": pipeline.predict(X_test)
}
)
df_results_test["diff"] = abs(df_results_test["true_value"] - df_results_test["predicted_value"])
df_results_test.sort_values("diff", ascending=False).head(20)
| true_value | predicted_value | diff | |
|---|---|---|---|
| 7252 | 7700000.0 | 2900098.750 | 4799901.250 |
| 3914 | 7062500.0 | 3157875.000 | 3904625.000 |
| 9254 | 6885000.0 | 3147814.250 | 3737185.750 |
| 4411 | 5570000.0 | 3001758.750 | 2568241.250 |
| 1448 | 5350000.0 | 3159702.000 | 2190298.000 |
| 1315 | 5300000.0 | 3352317.500 | 1947682.500 |
| 1164 | 5110800.0 | 3348500.750 | 1762299.250 |
| 8638 | 4489000.0 | 2940750.000 | 1548250.000 |
| 8092 | 4668000.0 | 3306771.500 | 1361228.500 |
| 2626 | 4500000.0 | 3201104.250 | 1298895.750 |
| 9487 | 2375000.0 | 1127361.250 | 1247638.750 |
| 14139 | 2110000.0 | 906920.500 | 1203079.500 |
| 656 | 3070000.0 | 1873606.000 | 1196394.000 |
| 21372 | 490000.0 | 1649058.625 | 1159058.625 |
| 21576 | 3567000.0 | 2420243.250 | 1146756.750 |
| 19484 | 2395000.0 | 1282102.625 | 1112897.375 |
| 5449 | 2850000.0 | 1774158.625 | 1075841.375 |
| 7432 | 2575000.0 | 1506080.000 | 1068920.000 |
| 18482 | 3650000.0 | 2591424.500 | 1058575.500 |
| 19684 | 2205000.0 | 1175083.375 | 1029916.625 |
| true_value | predicted_value | diff | |
|---|---|---|---|
| 12370 | 4208000.0 | 2.548266e+06 | 1.659734e+06 |
| 10446 | 3400000.0 | 1.952878e+06 | 1.447122e+06 |
| 7311 | 2500000.0 | 1.194972e+06 | 1.305028e+06 |
| 21050 | 900000.0 | 2.162562e+06 | 1.262562e+06 |
| 5617 | 2400000.0 | 1.201847e+06 | 1.198153e+06 |
| 19017 | 3800000.0 | 2.633888e+06 | 1.166112e+06 |
| 15258 | 3065000.0 | 1.920782e+06 | 1.144218e+06 |
| 13256 | 2546000.0 | 1.486281e+06 | 1.059719e+06 |
| 16302 | 3710000.0 | 2.653926e+06 | 1.056074e+06 |
| 10373 | 2983000.0 | 1.972321e+06 | 1.010679e+06 |
| 11535 | 3200000.0 | 2.200603e+06 | 9.993970e+05 |
| 19858 | 2700000.0 | 1.731232e+06 | 9.687684e+05 |
| 13020 | 2300000.0 | 1.371136e+06 | 9.288639e+05 |
| 5880 | 3418800.0 | 2.559992e+06 | 8.588085e+05 |
| 20295 | 3204000.0 | 2.347220e+06 | 8.567798e+05 |
| 10539 | 1700000.0 | 8.463644e+05 | 8.536356e+05 |
| 17558 | 2510000.0 | 1.658604e+06 | 8.513959e+05 |
| 15668 | 1680000.0 | 2.502938e+06 | 8.229380e+05 |
| 10468 | 2000000.0 | 1.182735e+06 | 8.172651e+05 |
| 11278 | 2100000.0 | 1.284781e+06 | 8.152186e+05 |
Busqueda de Hiperparametros xgb#
xgb_regressor = XGBRegressor(objective="reg:squarederror")
pipeline_xgb = Pipeline(steps=[
("preprocessor", preprocessor),
("model", xgb_regressor)
])
param_distributions = {
"model__max_depth": [3, 4, 5, 6],
"model__n_estimators": [100, 500, 1000],
"model__learning_rate": [0.0075, 0.01, 0.05],
"model__reg_alpha": [0, 5, 10, 15, 20],
"model__reg_lambda": [1, 10, 20, 30],
"model__subsample": [0.6, 0.8, 1.0],
"model__max_leaves": [100, 200, 300, 500]
}
random_search_xgb = RandomizedSearchCV(
estimator=pipeline_xgb,
param_distributions=param_distributions,
n_iter=10,
scoring="r2",
cv=5,
random_state=42,
n_jobs=-1,
return_train_score=True
)
random_search_xgb.fit(X_train, y_train)
print("Best parameters found: ", random_search_xgb.best_params_)
print(f"Best CV score: {random_search_xgb.best_score_}")
best_model = random_search_xgb.best_estimator_
print(f"R2 en Train: {best_model.score(X_train, y_train):.4f}")
print(f"R2 en Test: {best_model.score(X_test, y_test):.4f}")
pd.DataFrame(random_search_xgb.cv_results_)
Best parameters found: {'model__subsample': 0.8, 'model__reg_lambda': 1, 'model__reg_alpha': 10, 'model__n_estimators': 1000, 'model__max_leaves': 300, 'model__max_depth': 3, 'model__learning_rate': 0.05}
Best CV score: 0.8905389750992884
R2 en Train: 0.9461
R2 en Test: 0.8828
LightGBM (Light Gradient Boosting Machine)#
LightGBM es una implementación de Gradient Boosting diseñada para ser rápida, eficiente en el uso de memoria y capaz de manejar grandes volúmenes de datos con alta dimensionalidad. Es particularmente adecuada para problemas donde la velocidad y la escalabilidad son críticas.
Características principales#
Crecimiento de árboles basado en hojas (leaf-wise):
A diferencia de XGBoost, LightGBM divide las hojas con mayor ganancia en cada iteración, lo que puede generar árboles más profundos y precisos.
Ventaja: Mejora la eficiencia del modelo, especialmente en datos grandes.
Desafío: Mayor riesgo de sobreajuste en conjuntos de datos pequeños.
Divisiones basadas en histogramas:
Agrupa los valores continuos en histogramas, reduciendo significativamente el tiempo de cómputo.
Soporte nativo para variables categóricas:
Permite manejar variables categóricas directamente, sin necesidad de codificación adicional.
Uso eficiente de memoria:
Consume menos memoria que XGBoost gracias a su diseño basado en histogramas.
Hiperparámetros principales y su uso recomendado#
learning_rate(Coeficiente de aprendizaje):Controla la magnitud de las actualizaciones en cada iteración.
Recomendación: Usar valores bajos (
0.01a0.1) y compensar con un número alto de árboles (num_iterations).
max_depth(Profundidad máxima):Limita la profundidad de los árboles para evitar sobreajuste.
Recomendación: Usar
-1para desactivar la limitación, o valores bajos (5a10) para datos con ruido.
num_leaves(Número máximo de hojas):Controla la cantidad de divisiones posibles en un árbol.
Recomendación:
Valores iniciales como \(2^{\text{max\_depth}} - 1\).
Reducir este valor si hay sobreajuste.
min_child_samples(Tamaño mínimo de muestra en hojas):Número mínimo de datos requeridos para crear una hoja.
Impacto: Ayuda a controlar hojas pequeñas que pueden sobreajustarse a los datos de entrenamiento.
Recomendación:
Para datos grandes:
20a100.Para datos pequeños:
5a20.
Consejo: Incrementar este valor si el modelo muestra signos de sobreajuste.
min_data_in_leaf(Tamaño mínimo de muestra en hojas):Evita hojas muy pequeñas que pueden causar sobreajuste.
Recomendación:
Para datos grandes:
20a50.Para datos pequeños:
10o menos.
feature_fraction(Fracción de características por árbol):Porcentaje de características utilizadas en cada iteración.
Recomendación: Valores de
0.7a1.0.
bagging_fraction(Fracción de datos por iteración):Controla la proporción de datos de entrenamiento utilizados en cada árbol.
Recomendación:
0.7a0.9para reducir el riesgo de sobreajuste.Usar junto con
bagging_freqpara habilitar el muestreo.
reg_alpha(Regularización L1):Introduce una penalización L1 que fomenta la esparsidad en los pesos de las hojas, eliminando aquellas que son menos relevantes.
Impacto: Reduce el número de hojas efectivas en los árboles.
Recomendación:
Comenzar con valores bajos como
0.0o1.0y ajustar según el desempeño del modelo.
reg_lambda(Regularización L2):Controla la penalización L2 sobre los pesos de las hojas, reduciendo su magnitud.
Impacto: Suaviza las predicciones y previene que los pesos de las hojas crezcan demasiado.
Recomendación:
Valores iniciales entre
0.0y10.0.Incrementar si el modelo muestra sobreajuste.
min_gain_to_split(Ganancia mínima para división):
Controla las divisiones insignificantes en los árboles.
Recomendación:
Valores de
0.0(sin penalización) a0.1para datos más complejos.
Estrategia para el ajuste de hiperparámetros#
Comenzar con valores predeterminados:
LightGBM tiene configuraciones predeterminadas que suelen ser efectivas.
Ajustar primero
learning_rate,num_leaves, ymax_depth.
Validación cruzada:
Utilizar validación cruzada para medir el rendimiento y detectar sobreajuste o subajuste.
Pruebas de bagging y fracciones de características:
Probar con
bagging_fractionyfeature_fractionpara reducir el tiempo de entrenamiento y mejorar la generalización.
Exploración con Grid Search o Random Search:
Probar combinaciones sistemáticas o aleatorias de hiperparámetros para encontrar la mejor configuración.
Modelo LigthGBM#
lgbm = LGBMRegressor(verbose=-1)
pipeline_lgbm = Pipeline(steps=[
("preprocessor", preprocessor),
("model", lgbm)
])
pipeline_lgbm.fit(X_train, y_train)
print(pipeline_lgbm.score(X_train, y_train))
print(pipeline_lgbm.score(X_test, y_test))
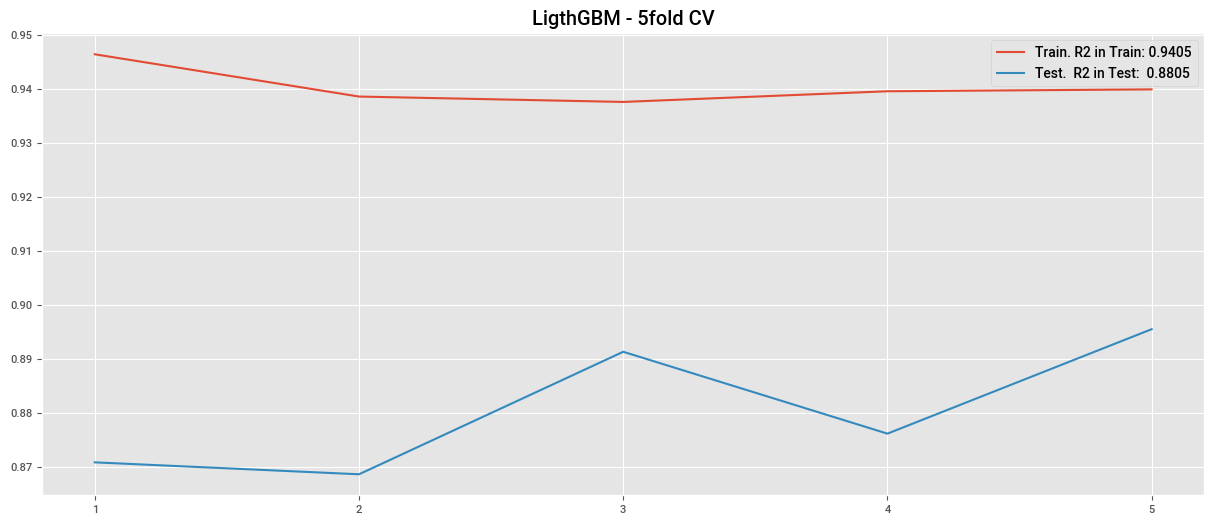
0.9392381025286636
0.8792562594391012
cv_lgbm = cross_validate(
lgbm,
X_train,
y_train,
cv=5,
scoring="r2",
return_train_score=True
)
plt.plot(cv_lgbm["train_score"], label=f"Train. R2 in Train: {cv_lgbm['train_score'].mean():.4f}")
plt.plot(cv_lgbm["test_score"], label=f"Test. R2 in Test: {cv_lgbm['test_score'].mean():.4f}")
plt.title("LigthGBM - 5fold CV")
plt.legend()
plt.xticks(np.arange(0,5), np.arange(1,6))
plt.show()
lgbm1 = LGBMRegressor(
objective="regression",
reg_alpha=25,
min_child_samples=150,
max_depth=4,
reg_lambda=30
)
pipeline_lgbm1 = Pipeline(steps=[
("preprocessor", preprocessor),
("model", lgbm1)
])
pipeline_lgbm1.fit(X_train, y_train)
print(pipeline_lgbm1.score(X_train, y_train))
print(pipeline_lgbm1.score(X_test, y_test))
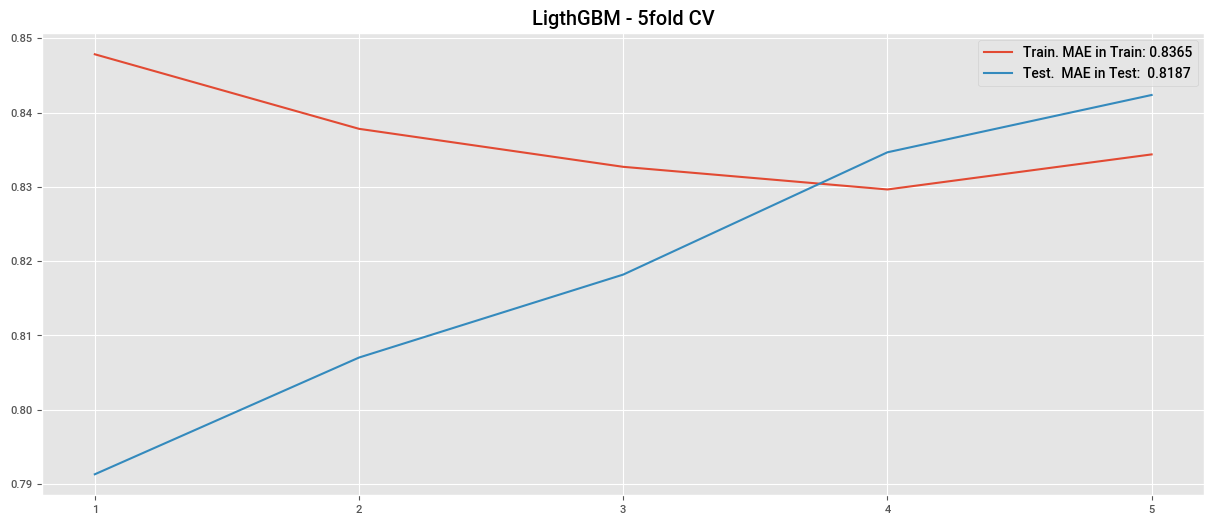
0.8438249657130915
0.8468238962295872
cv_lgbm1 = cross_validate(
pipeline_lgbm1,
X_train,
y_train,
cv=5,
scoring="r2",
return_train_score=True
)
plt.plot(cv_lgbm1["train_score"], label=f"Train. MAE in Train: {cv_lgbm1['train_score'].mean():.4f}")
plt.plot(cv_lgbm1["test_score"], label=f"Test. MAE in Test: {cv_lgbm1['test_score'].mean():.4f}")
plt.title("LigthGBM - 5fold CV")
plt.legend()
plt.xticks(np.arange(0,5), np.arange(1,6))
plt.show()
lgbm2 = LGBMRegressor(
objective="gamma",
reg_alpha=2,
min_child_samples=300,
learning_rate=0.0075,
reg_lambda=10,
n_estimators=1500,
max_depth=3,
subsample=0.9,
subsample_for_bin=1000,
num_leaves=300,
n_jobs=-1,
)
pipeline_lgbm2 = Pipeline(steps=[
("preprocessor", preprocessor),
("model", lgbm2)
])
pipeline_lgbm2.fit(X_train, y_train)
print(pipeline_lgbm2.score(X_train, y_train))
print(pipeline_lgbm2.score(X_test, y_test))
0.8239901867809278
0.8315345203942487
cv_lgbm2 = cross_validate(
pipeline_lgbm2,
X_train,
y_train,
cv=5,
scoring="r2",
return_train_score=True
)
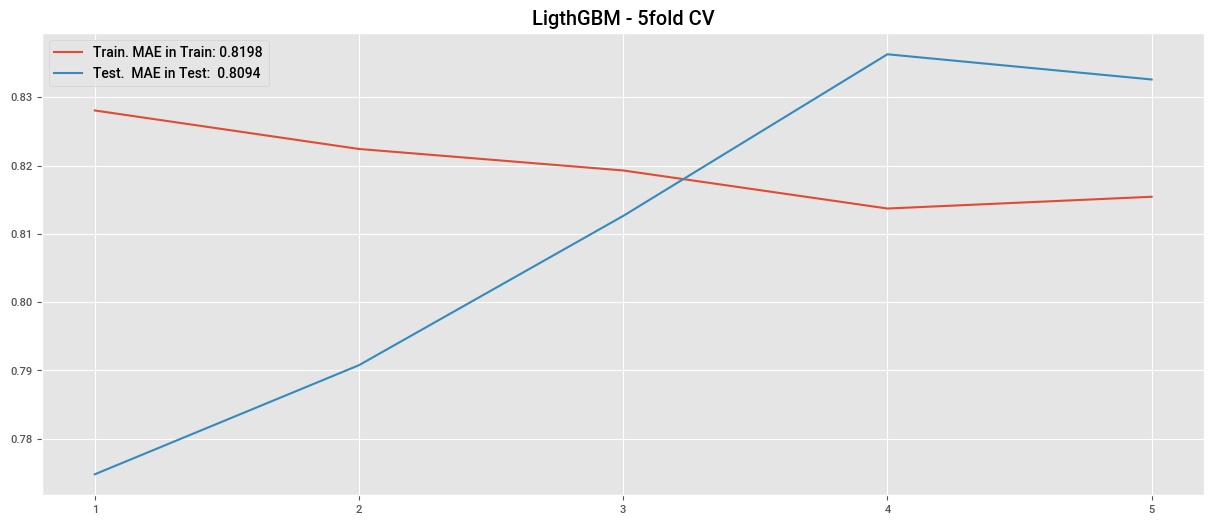
plt.plot(cv_lgbm2["train_score"], label=f"Train. MAE in Train: {cv_lgbm2['train_score'].mean():.4f}")
plt.plot(cv_lgbm2["test_score"], label=f"Test. MAE in Test: {cv_lgbm2['test_score'].mean():.4f}")
plt.title("LigthGBM - 5fold CV")
plt.legend()
plt.xticks(np.arange(0,5), np.arange(1,6))
plt.show()
px.scatter(
pd.DataFrame(
{
"true_value": y_test,
"predicted": pipeline_lgbm2.predict(X_test)
}
),
x="true_value",
y="predicted",
title="Prediccion VS Valor Real"
).show()
lgbm3 = LGBMRegressor(
objective="gamma",
reg_alpha=2,
min_child_samples=200,
learning_rate=0.01,
n_estimators=500,
max_depth=6,
subsample=0.9,
verbose=-1,
)
pipeline_lgbm3 = Pipeline(steps=[
("preprocessor", preprocessor),
("model", lgbm3)
])
pipeline_lgbm3.fit(X_train, y_train)
print(pipeline_lgbm3.score(X_train, y_train))
print(pipeline_lgbm3.score(X_test, y_test))
cv_lgbm3 = cross_validate(
pipeline_lgbm3,
X_train,
y_train,
cv=5,
scoring=("r2"),
return_train_score=True
)
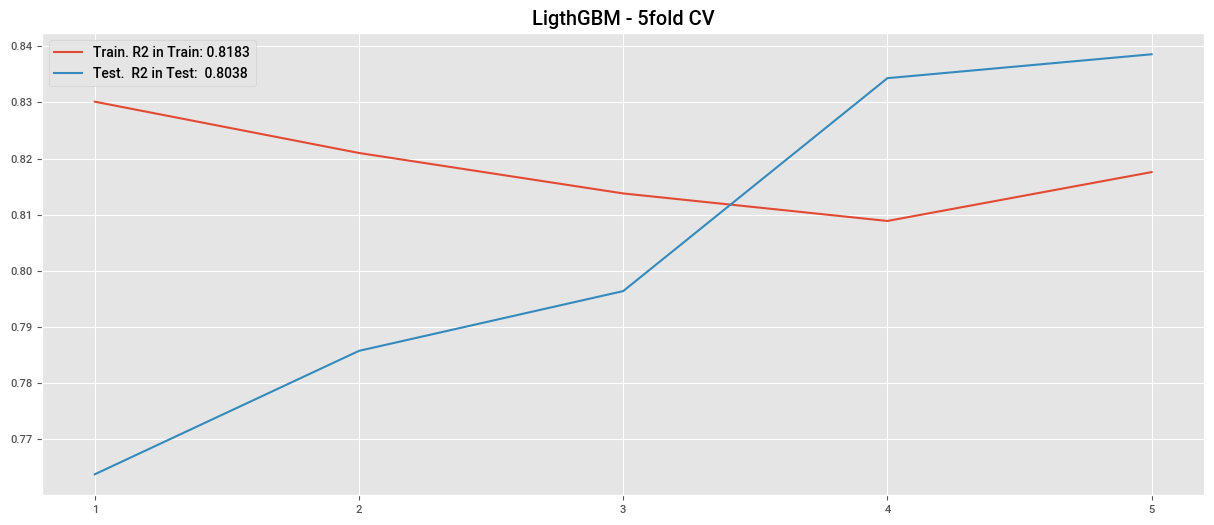
plt.plot(cv_lgbm3["train_score"], label=f"Train. R2 in Train: {cv_lgbm3['train_score'].mean():.4f}")
plt.plot(cv_lgbm3["test_score"], label=f"Test. R2 in Test: {cv_lgbm3['test_score'].mean():.4f}")
plt.title("LigthGBM - 5fold CV")
plt.legend()
plt.xticks(np.arange(0,5), np.arange(1,6))
plt.show()
0.8293522503882406
0.8401752759961569
lgbm = LGBMRegressor(verbose=-1)
pipeline_lgbm = Pipeline(steps=[
("preprocessor", preprocessor),
("model", lgbm)
])
param_distributions_lgbm = {
"model__objective": ["regression", "gamma"],
"model__num_leaves": [20, 31, 50, 100, 200],
"model__learning_rate": [0.005, 0.0075, 0.01, 0.02, 0.05],
"model__n_estimators": [100, 300, 500, 1000, 2000],
"model__max_depth": [2, 3, 4, 5],
"model__min_child_samples": [150, 155, 165, 175, 190, 200],
"model__min_split_gain": [0.0, 0.1, 0.2, 0.5],
"model__subsample": [0.7, 0.8, 0.9],
"model__reg_alpha": [1, 5, 10, 20],
"model__reg_lambda": [1, 5, 10, 20],
}
random_search_lgbm = RandomizedSearchCV(
estimator=pipeline_lgbm,
param_distributions=param_distributions_lgbm,
n_iter=5,
scoring="r2",
cv=5,
verbose=3,
random_state=42,
n_jobs=-1,
return_train_score=True
)
random_search_lgbm.fit(X_train, y_train)
print("Best parameters found: ", random_search_lgbm.best_params_)
print(f"Best CV score: {random_search_lgbm.best_score_:.4f}")
pd.DataFrame(random_search_lgbm.cv_results_)
Fitting 5 folds for each of 10 candidates, totalling 50 fits
CatBoost (Categorical Boosting)#
CatBoost es una implementación avanzada de Gradient Boosting desarrollada por Yandex, especializada en manejar variables categóricas de manera eficiente. Destaca por su facilidad de uso, configuraciones predeterminadas robustas y capacidad para evitar el sobreajuste.
Características principales#
Soporte nativo para variables categóricas:
A diferencia de otras bibliotecas, CatBoost maneja variables categóricas directamente, utilizando codificaciones como mean encoding supervisado de forma segura.
Boosting basado en órdenes:
En lugar de entrenar con los datos en su orden natural, utiliza permutaciones para mejorar la estabilidad y reducir el riesgo de sobreajuste.
Optimización eficiente:
Compatible con procesamiento en GPU, lo que acelera el entrenamiento en grandes conjuntos de datos.
Robustez frente a valores faltantes:
Puede manejar datos faltantes directamente, sin necesidad de preprocesarlos.
Hiperparámetros principales y su uso recomendado#
learning_rate(Coeficiente de aprendizaje):Controla la magnitud de las actualizaciones en cada iteración.
Recomendación: Usar valores bajos (
0.01a0.1) para evitar sobreajuste, especialmente en datos pequeños.
depth(Profundidad máxima):Define la profundidad máxima de los árboles.
Recomendación:
Valores entre
6y10funcionan bien para la mayoría de los casos.Reducir este valor para datos pequeños o con ruido.
iterations(Número de iteraciones o árboles):Determina cuántos árboles se entrenan secuencialmente.
Recomendación:
Usar valores entre
500y1000para modelos precisos.Ajustar según el
learning_rate: más iteraciones para valores bajos.
l2_leaf_reg(Regularización L2):Controla la penalización L2 aplicada a los pesos de las hojas.
Recomendación:
Comenzar con valores entre
3y10.Incrementar si se observa sobreajuste.
bagging_temperature:Controla la aleatoriedad en la selección de muestras para cada iteración.
Recomendación:
Usar valores bajos (
0.0a1.0) para datos grandes.Incrementar para datos más pequeños o ruidosos.
border_count:Define el número de divisiones utilizadas para variables numéricas.
Recomendación:
Comenzar con
128.Reducir para conjuntos de datos pequeños o si el tiempo de entrenamiento es un problema.
Estrategia para el ajuste de hiperparámetros#
Comenzar con configuraciones predeterminadas:
CatBoost tiene parámetros predeterminados sólidos que funcionan bien en muchos problemas.
Ajustar iteraciones y
learning_rate:Usar un valor bajo de
learning_rate(0.01a0.1) y aumentar las iteraciones para lograr un ajuste más preciso.
Probar diferentes profundidades (
depth):Probar valores entre
6y10dependiendo de la complejidad de los datos.
Usar validación cruzada:
Evaluar el modelo en varias particiones para detectar sobreajuste o subajuste.
Explorar con Grid Search o Random Search:
Probar combinaciones de parámetros clave como
depth,l2_leaf_reg, ybagging_temperature.
Modelo con CatBoostRegressor.#
catboost = CatBoostRegressor(
loss_function="RMSE",
cat_features=features_categoric,
learning_rate=0.0075,
n_estimators=2500,
min_child_samples=150,
reg_lambda=150,
max_depth=3,
subsample=0.8,
random_state=42,
verbose=0
)
catboost.fit(X_train, y_train)
print(f"\nR2 en Train: {catboost.score(X_train, y_train):.4f}")
print(f"R2 en Test: {catboost.score(X_test, y_test):.4f}")
df_plot = pd.DataFrame({"true_value": y_test, "predicted": catboost.predict(X_test)})
px.scatter(df_plot, x="true_value", y="predicted")
cv_catboost = cross_validate(
catboost,
X_train,
y_train,
cv=5,
scoring="r2",
return_train_score=True
)
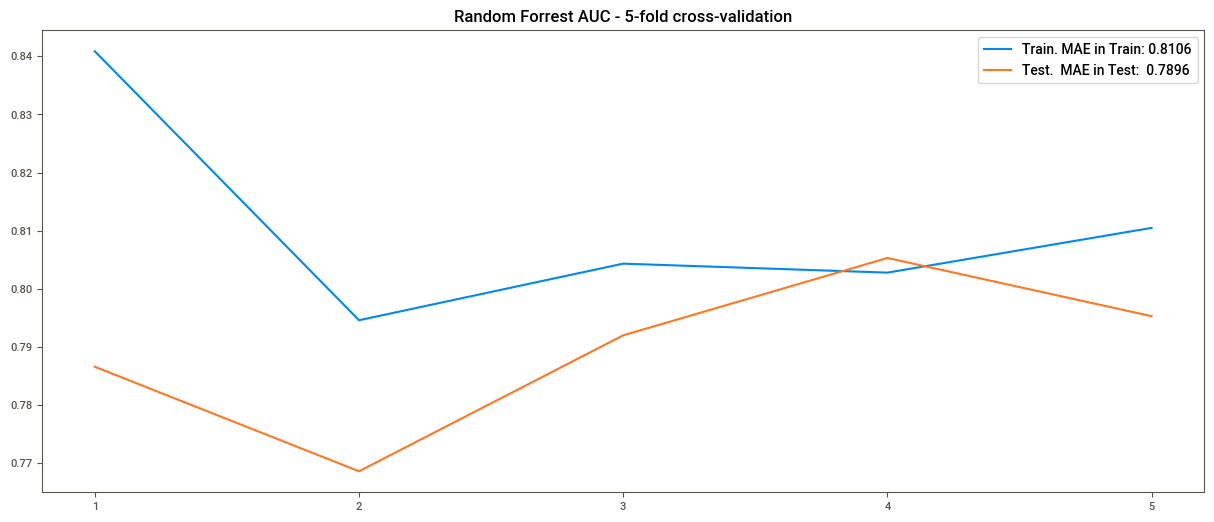
plt.plot(cv_catboost["train_score"], label=f"Train. MAE in Train: {cv_catboost['train_score'].mean():.4f}")
plt.plot(cv_catboost["test_score"], label=f"Test. MAE in Test: {cv_catboost['test_score'].mean():.4f}")
plt.title("CatBoostRegressor - 5-fold cross-validation")
plt.legend()
plt.xticks(np.arange(0,5), np.arange(1,6))
plt.show()
R2 en Train: 0.8137
R2 en Test: 0.8018
pipeline_catboost = Pipeline(steps=[
("model", catboost)
])
pipeline_catboost.fit(X_train, y_train)
print(pipeline_catboost.score(X_train, y_train))
print(pipeline_catboost.score(X_test, y_test))
0.8137006861318932
0.8017986205122258
catboost = CatBoostRegressor(cat_features=features_categoric, verbose=0)
pipeline_catboost = Pipeline(steps=[
("model", catboost)
])
param_distributions = {
"model__iterations": [100, 300, 500, 1000, 2000],
"model__learning_rate": [0.005, 0.075, 0.01, 0.02, 0.05],
"model__depth": [2, 3, 4, 5, 6],
"model__l2_leaf_reg": [1, 3, 5, 7, 9],
"model__bagging_temperature": [0, 0.1, 0.2, 0.5, 1.0],
"model__loss_function": ["MAE", "RMSE", "MAPE"]
}
random_search_catboost = RandomizedSearchCV(
estimator=pipeline_catboost,
param_distributions=param_distributions,
n_iter=5,
scoring="r2",
cv=5,
random_state=42,
n_jobs=-1,
return_train_score=True
)
random_search_catboost.fit(X_train, y_train)
print("Best parameters found: ", random_search_catboost.best_params_)
print("Best CV score R2: ", random_search_catboost.best_score_)
best_model = random_search_catboost.best_estimator_
print(best_model.score(X_train, y_train))
print(best_model.score(X_test, y_test))
pd.DataFrame(random_search_catboost.cv_results_)
