PCA: otros ejemplos y algunas funciones útiles.

Universidad Central

Maestría en analítica de datos

Métodos estadísticos para analítica de datos.

Docente: Luis Andrés Campos Maldonado.

Idea central:

Se tiene un conjunto de \(p\) features cuantitativas y se quieren construir un numero de features \(r\leq p\) con independencia lineal y ortogonales, que contengan la mayor cantidad de variabilidad en el dataset.

Términos clave para el análisis de componentes principales.

• Componente principal: Una combinación lineal de las features originales.

• Loading: Los pesos que transforman las features originales en las componentes principales.

• Gráfico de sedimentación: Un plot de las varianzas de las componentes, que muestra la importancia relativa de las componentes, ya sea como varianza explicada o como proporción de la varianza explicada.

Representación de Variables Originales en un Biplot de PCA

El Análisis de Componentes Principales (PCA) es una técnica estadística utilizada para reducir la dimensionalidad de un conjunto de datos, conservando la mayor parte de la varianza. Este proceso implica encontrar nuevas variables (componentes principales) que son combinaciones lineales de las variables originales.

Matriz de Datos Originales

Supongamos que tenemos un conjunto de datos \(\mathbf{X}\) con \(m\) observaciones y \(n\) variables originales. La matriz \(\mathbf{X}\) tiene la forma:

\[\begin{split} \mathbf{X} = \begin{pmatrix} x_{11} & x_{12} & \dots & x_{1n} \\ x_{21} & x_{22} & \dots & x_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ x_{m1} & x_{m2} & \dots & x_{mn} \end{pmatrix} \end{split}\]

Antes de realizar el PCA, centramos los datos restando la media de cada variable:

\[ \mathbf{X}_c = \mathbf{X} - \mathbf{1}\mu^\top \]

Aquí, \(\mathbf{X}_c\) es la matriz centrada, \(\mathbf{1}\) es un vector columna de unos (de tamaño \(m\)), y \(\mu\) es el vector de medias de cada variable.

Descomposición en Componentes Principales

Cálculo de la Matriz de Covarianza

Se calcula la matriz de covarianza \(\mathbf{C}\) de \(\mathbf{X}_c\):

\[ \mathbf{C} = \frac{1}{m-1} \mathbf{X}_c^\top \mathbf{X}_c \]

Eigenvalores y Eigenvectores

Realizamos la descomposición en valores propios de \(\mathbf{C}\):

\[ \mathbf{C} \mathbf{v}_i = \lambda_i \mathbf{v}_i \]

• \(\lambda_i\) son los eigenvalores, que indican la varianza explicada por cada componente principal.

• \(\mathbf{v}_i\) son los eigenvectores, que representan las direcciones principales en el espacio original de las \(n\) variables.

Proyección de los Datos

Las nuevas coordenadas de las observaciones en el espacio de las componentes principales se obtienen proyectando los datos centrados sobre los eigenvectores:

\[ \mathbf{Z} = \mathbf{X}_c \mathbf{V}_k \]

Aquí, \(\mathbf{Z}\) es la matriz de componentes principales, y \(\mathbf{V}_k\) es la matriz de eigenvectores correspondientes a las \(k\) primeras componentes principales.

Representación de las Variables Originales en el Biplot

Matriz de Cargas

La matriz \(\mathbf{V}_k\) se conoce como la matriz de cargas. Sus elementos \(v_{ij}\) indican cómo las variables originales contribuyen a las componentes principales:

\[\begin{split} \mathbf{V}_k = \begin{pmatrix} v_{11} & v_{12} & \dots & v_{1k} \\ v_{21} & v_{22} & \dots & v_{2k} \\ \vdots & \vdots & \ddots & \vdots \\ v_{n1} & v_{n2} & \dots & v_{nk} \end{pmatrix} \end{split}\]

Cada fila \(\mathbf{v}_j\) representa las cargas de la \(j\)-ésima variable original en las \(k\) componentes principales seleccionadas.

Proyección de Variables en el Espacio de las Componentes Principales

Para representar las variables originales en un biplot (cuando \(k = 2\)):

1. Selecciona las columnas de \(\mathbf{V}_k\) correspondientes a las dos primeras componentes principales, \(\mathbf{v}_1\) y \(\mathbf{v}_2\).

2. La proyección de la \(j\)-ésima variable original en el biplot se representa por el punto \((v_{j1}, v_{j2})\), donde:

   • \(v_{j1}\) es la carga de la \(j\)-ésima variable en la primera componente principal.

   • \(v_{j2}\) es la carga de la \(j\)-ésima variable en la segunda componente principal.

Visualización en el Biplot

Para cada variable \(j\), se dibuja un vector desde el origen hasta el punto \((v_{j1}, v_{j2})\). Estos vectores en el biplot indican:

• Dirección: Hacia dónde “apunta” la variable en relación con las componentes principales.

• Longitud: Cuánta varianza de la variable original es capturada por las dos primeras componentes principales.

Interpretación

• Ángulo entre vectores: Indica la correlación entre las variables originales.

• Longitud del vector: Indica la contribución de la variable a las componentes principales seleccionadas.

• Dirección: Muestra cómo se relaciona cada variable con las nuevas dimensiones definidas por las componentes principales.

Resumen

En un biplot, los vectores que representan las variables originales son el resultado de proyectar estas variables en el espacio definido por las componentes principales seleccionadas. Esta proyección se realiza utilizando la matriz de cargas, y los vectores resultantes permiten visualizar e interpretar cómo las variables originales contribuyen a la estructura de varianza capturada en el espacio de las componentes principales.

Protocolo de módulos PCA.

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import plotly.express as px
import plotly.graph_objects as go
import warnings
##
from sklearn.decomposition import PCA            ## Principal component analysis.
from sklearn.preprocessing import StandardScaler ## Escalar datos.
from utils.plots_pca import *
##
warnings.filterwarnings('ignore')
plt.rcParams['figure.figsize'] = (15, 9)
plt.style.use('ggplot')

Construcción de algunas funciones auxiliares

En los siguientes bloques de código se muestran algunas funciones que pueden de ser de ayuda para el ánalisis de PCA en Python.

Todas fueron construidas por el autor de este cuaderno, con apoyo del material de la página oficial de plotly, tenga la libertad de entenderla, mejorarla y por supuesto compartir dicha mejoras.

• biplot Esta función genera un biplot donde se muestran los espacios de individuos y las variables en un solo plot.

• biplot1: Esta función genera solo el primer plano factorial donde se aprecia la influencia de la features originales en dicho plano,

• view_index: Permite seleccionar algunos registros del dataframe en pro de un mejor entendimiento de los plots anteriores.

• sedimentacion: Genera el gráfico de sedimentación para buscar un posible método para la selección de la cantidad de componenetes principales.

• plot_loadings_heatmap(): Genera un barplot de las cargas en cada una de las componentes principales.

• plot_loadings_bar(): Esta función genera un heatmap de los loadings de las componentes pricipales.

Ejemplo 1

El dataset birds.txt contiene medidas corporales de aves, se desea buscar realizar un análisis de la selección natural.

Se tiene una información adicional sobre el índice de los registros, de la ave 1 a la 21 sobrevivieron.

url_base = "https://raw.githubusercontent.com/lacamposm/Metodos_Estadisticos/main/data/"
df_name1 = "birds.txt"
df1 = pd.read_csv(url_base + df_name1, sep = " ", index_col = 0,)
df1.head()

	longitud_total	extension_alas	longitud_pico_y_cabeza	longitud_humero	longitud_quilla
pajaro
1	156	245	31.6	18.5	20.5
2	154	240	30.4	17.9	19.6
3	153	240	31.0	18.4	20.6
4	153	236	30.9	17.7	20.2
5	155	243	31.5	18.6	20.3

sns.heatmap(df1.corr(), annot=True, cmap="PuBu")
plt.show()

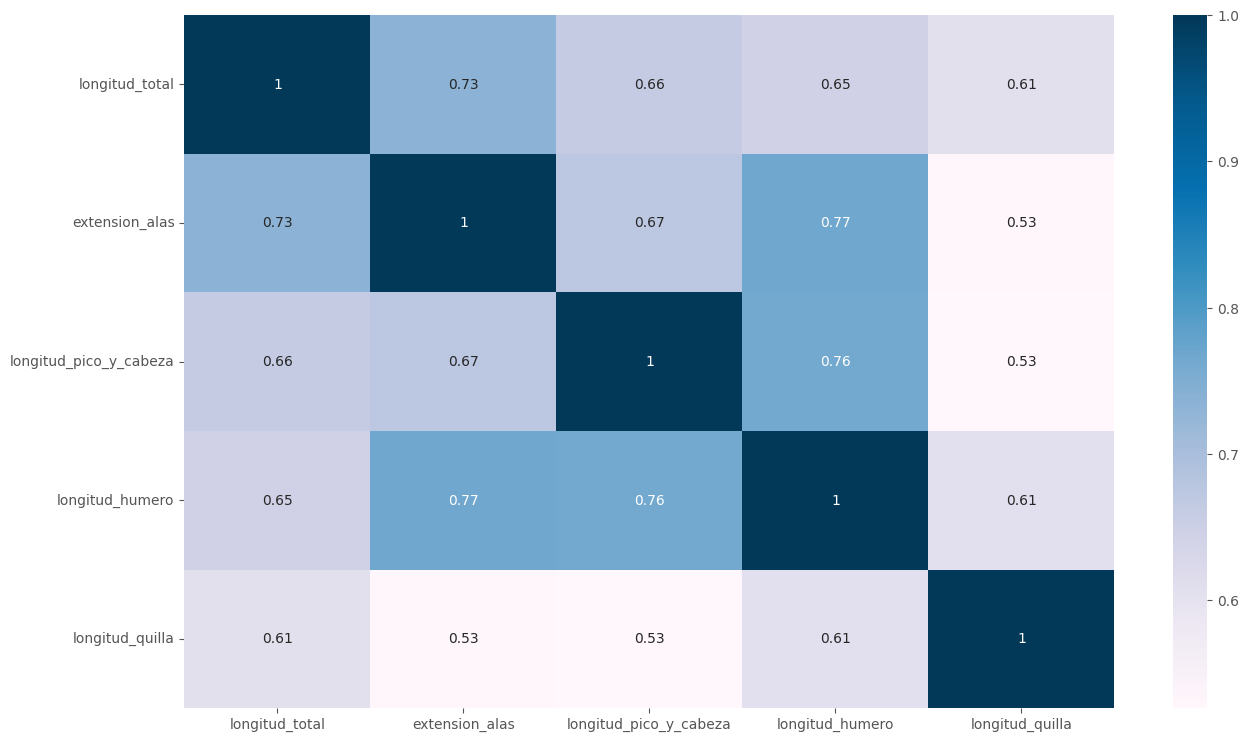
Podemos observar una alta correlación lineal entre las variables, podemos pensar que un PCA podría estar bastaste bien en este caso.

# Rutina habitual.
scaler1 = StandardScaler()
scaler1.fit(df1)
X_scaled1 = scaler1.transform(df1)

display(pd.DataFrame(X_scaled1, columns=df1.columns))

pca1 = PCA()
pca1.fit(X_scaled1)

	longitud_total	extension_alas	longitud_pico_y_cabeza	longitud_humero	longitud_quilla
0	-0.547333	0.732373	0.179019	0.054812	-0.332785
1	-1.100309	-0.264468	-1.346531	-1.019498	-1.250023
2	-1.376796	-0.264468	-0.583756	-0.124240	-0.230870
3	-1.376796	-1.061941	-0.710885	-1.377602	-0.638531
4	-0.823821	0.333637	0.051889	0.233863	-0.536616
5	1.388081	1.131110	0.687535	0.950070	0.074877
6	-0.270845	-0.663205	-0.710885	-0.124240	-0.638531
7	-0.823821	-0.463836	1.704568	0.233863	0.380623
8	1.664569	1.330478	1.577439	1.129122	0.278707
9	0.005643	-0.663205	-0.583756	0.591967	1.195946
10	0.005643	-0.264468	-0.202369	0.233863	1.195946
11	0.558618	0.533005	-0.456627	0.233863	-0.332785
12	0.835106	0.931742	1.068923	1.487225	0.992115
13	-0.270845	0.732373	0.687535	1.129122	-0.842362
14	-0.270845	-1.261309	0.051889	-0.661395	-1.046193
15	-0.547333	-0.862573	-0.710885	-0.840447	-0.536616
16	0.005643	0.533005	-0.075240	0.054812	0.788284
17	-1.376796	-0.663205	-1.219402	-0.482343	0.074877
18	-0.823821	-1.061941	-1.473660	0.054812	-0.740446
19	1.388081	0.931742	1.323181	0.233863	1.094030
20	0.282130	-1.061941	0.051889	-0.840447	0.686369
21	-0.823821	-0.264468	-0.075240	-0.840447	-0.128954
22	-0.547333	-0.264468	0.051889	-0.482343	-0.230870
23	0.558618	0.134268	1.450310	0.591967	0.890200
24	-1.653284	-1.859414	-1.473660	-2.272860	-1.046193
25	0.558618	1.729215	0.306148	0.591967	1.705523
26	-0.823821	-0.862573	-0.583756	0.054812	-0.842362
27	-0.270845	0.732373	0.941793	1.845328	0.584454
28	1.941057	0.732373	2.085956	2.382483	1.909353
29	-1.376796	-2.058783	-1.727919	-2.093808	-1.046193
30	1.111594	-0.463836	-1.473660	-0.840447	2.317015
31	1.111594	0.333637	0.179019	0.591967	0.482538
32	0.282130	0.732373	0.433277	0.054812	0.890200
33	0.282130	1.131110	-0.710885	-0.661395	-1.861516
34	-0.823821	0.333637	-0.710885	0.054812	0.482538
35	1.111594	2.127951	0.560406	1.129122	1.399777
36	-1.653284	-2.258151	-1.346531	-2.093808	-2.269177
37	0.282130	0.134268	-0.838015	-0.482343	-0.332785
38	-0.823821	-0.663205	-0.329498	-1.019498	-1.555770
39	1.388081	1.529846	2.467343	1.845328	2.011269
40	1.388081	0.134268	-0.583756	-0.661395	-0.128954
41	-0.547333	-0.862573	0.306148	-0.482343	-0.536616
42	0.282130	-0.663205	0.051889	-0.124240	-0.536616
43	0.835106	0.732373	0.814664	1.129122	-0.027039
44	-0.823821	-1.261309	-0.965144	-1.377602	-1.250023
45	1.111594	1.131110	0.560406	1.129122	-0.434700
46	-1.376796	-0.862573	-1.092273	0.233863	-0.434700
47	1.111594	0.732373	1.323181	0.054812	0.278707
48	1.664569	1.330478	1.068923	0.591967	0.074877

PCA()

In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.

# Plot de sediementación
sedimentacion(pca1)

Notemos la forma de codo que se presenta en la gráfica, dado que no hay un método puntual para la selección de las componentes principal, podemos optar por incluir cierta cantidad de varibilidad (un valor determinado) o determinar el número de componentes principales observando si hasta determinado punto la inclusión de una variable adicional tiene un peso significativo, recuerde que a más variables la interpretabilidad se vuelve bastante complicada.

Basados en lo anterior vamos a considerar vamos a conciderar solo 2 componentes principales.

print(pca1.explained_variance_)
print(pca1.explained_variance_ratio_)
print(np.cumsum(pca1.explained_variance_ratio_))

[3.69131123 0.54257708 0.39447506 0.30784813 0.16795517]
[0.72319567 0.10630082 0.07728491 0.0603131  0.0329055 ]
[0.72319567 0.82949648 0.90678139 0.9670945  1.        ]

n_components = 2
pca1 = PCA(n_components=n_components)
pca1.fit(X_scaled1)

PCA(n_components=2)

In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.

expl = pca1.explained_variance_ratio_*100
print("""Con las {} primeras componentes principales, la cantidad de varianza explicada es: {:.2f}% 
      """.format(n_components,sum(expl[0: n_components])))

Con las 2 primeras componentes principales, la cantidad de varianza explicada es: 82.95% 
      

# Loadings.
plot_loadings_heatmap(pca1, df1)

Recuerde que los valores que se generan apartir de la primera componente principal es una combinación lineal de la forma:

\[Y_1 = 0.45*longitudTotal +0.46*exetensionAlas+0.45*longitudPicoCebeza+0.47*longitudHumero+0.4*longitudQuilla\]

Vemos que todos los coeficientes son positivos, y además, aproximadamente el \(72.3\%\) de la variación está relacionada con las diferencias de tamaño, luego \(Y_1\) es un indicador del tamaño de las aves.

De manera completamente análoga, \(Y_2\), reúne las variables que registran la forma de las aves, pues se contrastan las features: extensión de las alas, longitud de pico y cabeza, extensión del húmero con longitud de la quilla. Mientras el primer grupo aumenta, la longitud de la quilla disminuye y viceversa.

La información transformada se encuentra es el siguiente código.

pca1_trans = pca1.transform(X_scaled1)
pca1_trans =  pd.DataFrame(pca1_trans, index=df1.index, columns=["PC1","PC2"])
pca1_trans.head()

	PC1	PC2
pajaro
1	0.064955	-0.607064
2	-2.202907	-0.446884
3	-1.157437	0.019454
4	-2.335015	0.173775
5	-0.298100	-0.672101

print("Se ajustó un PCA a una data de tamaño:",df1.shape)
print("Se obtuvo un ajuste por PCA de tamaño:",pca1_trans.shape)

Se ajustó un PCA a una data de tamaño: (49, 5)
Se obtuvo un ajuste por PCA de tamaño: (49, 2)

biplot(pca1,df1)

Teniendo en cuenta lo comentado en el párrafo anterior, la ave número 31 (arriba en el centro) tiene el valor más alto respecto a la longitud de la quilla. Las aves 30, 25, 37 (a la izquierda) tienen valores bajos (con respecto a la medía) en varias features (muchas ponderan en el primer componente principal). En constraste tenemos las aves 29, 40. La ave “propotípo” esta en el centro del plot (ave 41).

df1.mean()

longitud_total            157.979592
extension_alas            241.326531
longitud_pico_y_cabeza     31.459184
longitud_humero            18.469388
longitud_quilla            20.826531
dtype: float64

view_index(df1, [31,30,25,37,29,40])

	longitud_total	extension_alas	longitud_pico_y_cabeza	longitud_humero	longitud_quilla
31	162.0	239.0	30.3	18.0	23.1
30	153.0	231.0	30.1	17.3	19.8
25	152.0	232.0	30.3	17.2	19.8
37	152.0	230.0	30.4	17.3	18.6
29	165.0	245.0	33.1	19.8	22.7
40	163.0	249.0	33.4	19.5	22.8

El siguiente plot:

biplot1(pca1, df1)

se puede observar como el primer eje en el plano factorial está influenciado por la longitud del húmero y la longitud total, para el segundo eje factorial, longitud de la quilla y longitud del pico y cabeza.

## Selección natural.
temp = pca1_trans.copy()
temp["sobrevivio"] = ["vivo" if x<22 else "muerto" for x in df1.index.values]

px.scatter(
    temp,
    x="PC1",
    y="PC2",
    color="sobrevivio"
)

Ejercicio en clase.

Realizar un PCA con la base de emisiones y teniendo como individuo el año. Realice toda la rutina presentada en clase, busque generar sus propios análisis haciendo uso de las nuevas herramientas presentados en este cuaderno.

Retomando un ejemplo anterior.

Consideremos el dataset Global_Carbon_Budget_2018.csv.

url_base = "https://raw.githubusercontent.com/lacamposm/Metodos_Estadisticos/main/data/"
df_name = "Global_Carbon_Budget_2018.csv"
df = pd.read_csv(url_base + df_name, sep=";", decimal=",", index_col = "Year")
df.head()

	fossil fuel and industry	land-use change emissions	atmospheric growth	ocean sink	land sink	budget imbalance
Year
1750	NaN	NaN	-0.08	NaN	0.09	NaN
1751	0.0	NaN	-0.07	NaN	-0.53	NaN
1752	0.0	NaN	-0.07	NaN	-0.27	NaN
1753	0.0	NaN	-0.07	NaN	-0.17	NaN
1754	0.0	NaN	-0.06	NaN	-0.33	NaN

feature	Traducción
fossil fuel and industry	Combustible fósil e industría
land-use change emissions	emisiones de cambio de uso de la tierra
atmospheric growth	crecimiento atmosférico
ocean sink	sumidero del oceano
land sink	sumidero de tierra
budget imbalance	desequilibrio presupuestario

## Rutina escalamiento.
df_pca = df.drop(columns=["budget imbalance"])
df_pca = df_pca.dropna()            
scaler = StandardScaler()           
scaler.fit(df_pca)                  
X_scaled = scaler.transform(df_pca)

pd.DataFrame(X_scaled, index=df_pca.index, columns=df_pca.columns).corr()

	fossil fuel and industry	land-use change emissions	atmospheric growth	ocean sink	land sink
fossil fuel and industry	1.000000	0.404771	0.969705	0.988774	0.727075
land-use change emissions	0.404771	1.000000	0.293668	0.426617	0.295279
atmospheric growth	0.969705	0.293668	1.000000	0.966279	0.711759
ocean sink	0.988774	0.426617	0.966279	1.000000	0.726006
land sink	0.727075	0.295279	0.711759	0.726006	1.000000

# Rutina PCA
pca = PCA()
pca.fit(X_scaled)                   
pca_array = pca.transform(X_scaled)

# Plot de sedimentación
sedimentacion(pca)

name_columns = [f"PC{i+1}" for i in range(0,pca_array.shape[1])]
pca_trans =  pd.DataFrame(pca_array, index = df_pca.index, columns = name_columns)
pca_trans.head()

	PC1	PC2	PC3	PC4	PC5
Year
1850	-2.095784	-1.196339	0.250146	-0.083911	0.128713
1851	-2.381818	-1.092507	-0.303762	-0.142315	0.118502
1852	-2.263906	-1.095204	-0.005834	-0.179125	0.122529
1853	-2.378335	-1.053040	-0.175729	-0.224897	0.123368
1854	-2.352181	-1.059783	-0.066733	-0.261231	0.126965

pca.components_

array([[ 0.50625924,  0.25177241,  0.49391515,  0.50715776,  0.42326242],
       [-0.08557012,  0.95984491, -0.2149806 , -0.0587595 , -0.14733009],
       [-0.24669646,  0.03728889, -0.28105587, -0.24452182,  0.89384958],
       [-0.41578379,  0.11667435,  0.79418177, -0.42733142,  0.01319523],
       [ 0.70897393,  0.01746506, -0.01068107, -0.70493636, -0.0012577 ]])

# Plot loadings.
plot_loadings_heatmap(pca,df_pca,n_compo=5)

plot_loadings_bar(pca, df_pca, n_compo=5, rotation=40)

biplot(pca, df_pca)

df_pca.mean()

fossil fuel and industry     1.999677
land-use change emissions    1.182645
atmospheric growth           1.204452
ocean sink                   0.834645
land sink                    1.008129
dtype: float64

view_index(df_pca,[1867,1958,1997,1999])

	fossil fuel and industry	land-use change emissions	atmospheric growth	ocean sink	land sink
1867	0.13	0.67	0.39	0.25	0.55
1958	2.33	1.79	1.02	0.81	-0.06
1997	6.53	1.78	3.39	2.14	2.98
1999	6.53	1.20	3.43	2.28	3.70

biplot1(pca,df_pca)

Ejemplo 2.

Vamos a considerar el dataframe Delitos_Colombia.csv que contiene el número de delitos por departamento, en distintas categorías. Toda la información es numérica.

url_base = "https://raw.githubusercontent.com/lacamposm/Metodos_Estadisticos/main/data/"
df_name2 = "Delitos_Colombia.csv"
df2 = pd.read_csv(url_base + df_name2, sep=";", decimal=",", index_col=0)
df2.head()

	Delitos_Sexuales	Homicidios	Transito	Asalto	Intrafamiliar	Poblacion
Departamento
Antioquia	2163	375	5079	11897	8205	6690977
Atlantico	1042	85	1928	59	3659	2546138
Bogota_D.C.	4211	1463	725	2725	19811	8181047
Bolivar	944	28	922	3812	2085	2171558
Boyaca	517	95	1167	4084	2707	1281979

df2.describe().T

	count	mean	std	min	25%	50%	75%	max
Delitos_Sexuales	33.0	6.484545e+02	8.246769e+02	0.0	204.0	420.0	616.0	4211.0
Homicidios	33.0	1.161818e+02	2.596099e+02	0.0	17.0	58.0	81.0	1463.0
Transito	33.0	1.173667e+03	1.371468e+03	0.0	143.0	861.0	1248.0	5599.0
Asalto	33.0	2.816121e+03	3.001322e+03	1.0	654.0	2243.0	3766.0	11897.0
Intrafamiliar	33.0	2.059242e+03	3.590915e+03	2.0	411.0	1083.0	2142.0	19811.0
Poblacion	33.0	1.510143e+06	1.827319e+06	43446.0	375258.0	1040193.0	1788648.0	8181047.0

# Seleccionamos las cuantitativas (ACP solo trabaja con cuantitativas). Cuando sea el caso seleccionamos 
# así: -----> cuanti = df2.select_dtypes(np.number)

sns.heatmap(df2.corr(), annot = True, cmap = "PuBu")
plt.show()

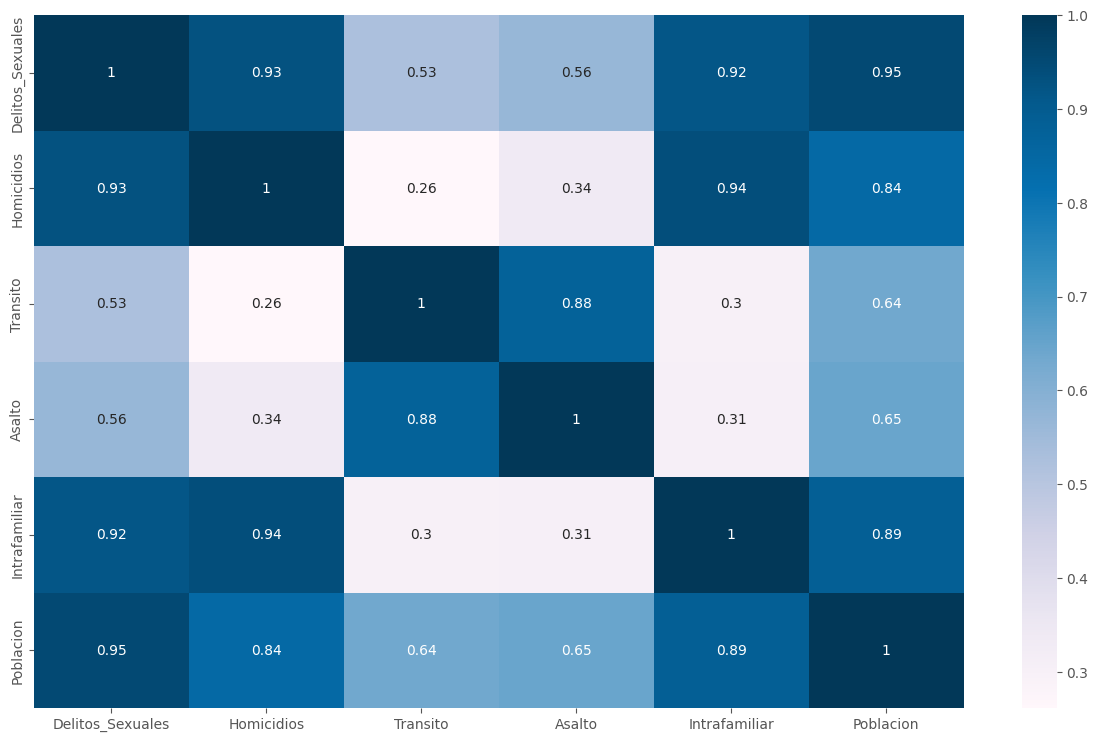
Notemos que las diferencias en las desviaciones en las distintas features es bastante alta, debemos por tanto realizar unas “mejoras” en nuestro dataset.

1. Para realizar un mejor análisis vamos considerar la siguiente tasa (para todas las variables):

\[Tasa Delitos Sexuales=100.000\times \frac{Delitos Sexuales}{Poblacion}\]

la cual representa la incidencia por cada \(100.000\) habitantes.

df2_pca = df2.copy()
df2_pca["DSex_p"] = 100000*df2_pca["Delitos_Sexuales"]/df2_pca["Poblacion"]
df2_pca["DHom_p"] = 100000*df2_pca["Homicidios"]/df2_pca["Poblacion"]
df2_pca["DIntra_p"] = 100000*df2_pca["Intrafamiliar"]/df2_pca["Poblacion"]
df2_pca["DTransi_p"] = 100000*df2_pca["Transito"]/df2_pca["Poblacion"]
df2_pca["DAsal_p"] = 100000*df2_pca["Asalto"]/df2_pca["Poblacion"]
df2_pca = df2_pca[["DSex_p", "DHom_p", "DIntra_p", "DTransi_p", "DAsal_p"]]
df2_pca

	DSex_p	DHom_p	DIntra_p	DTransi_p	DAsal_p
Departamento
Antioquia	32.327118	5.604563	122.627831	75.908197	177.806619
Atlantico	40.924726	3.338389	143.707843	75.722526	2.317235
Bogota_D.C.	51.472629	17.882797	242.157269	8.861946	33.308695
Bolivar	43.471093	1.289397	96.014014	42.457996	175.542168
Boyaca	40.328274	7.410418	211.157905	91.031132	318.569961
Caldas	44.573234	6.540091	98.101361	125.569743	225.683439
Caqueta	44.532928	3.627116	90.476402	24.382282	131.785226
Cauca	29.657980	4.378083	104.156001	60.798859	167.920658
Cesar	52.644568	4.128986	131.564501	79.013773	258.718494
Cordoba	29.631319	0.782714	36.172573	49.255080	95.938385
Cundinamarca	52.028394	12.873372	22.359015	91.611340	367.051584
Choco	30.863838	0.388224	56.874871	19.605331	102.491236
Huila	41.602307	5.680636	184.286525	92.143262	318.700404
La_Guajira	30.667386	2.595672	72.390412	18.650385	119.593191
Magdalena	38.504130	1.925206	141.849215	53.135699	230.485722
Meta	81.245475	9.245853	272.359227	108.491234	370.424286
narigno	10.998723	4.255787	82.960215	98.988504	199.248218
Norte_de_Santander	26.880059	4.887283	156.968044	76.830970	235.883297
Quindio	69.570057	14.087937	169.750939	211.666899	354.633366
Risaralda	55.797805	7.543037	144.247660	222.054599	232.594185
Santander	62.127724	8.943714	19.035284	156.730216	357.461592
Sucre	46.064874	1.938373	123.485788	30.899953	192.469077
Tolima	43.381595	4.788877	150.849638	186.132397	300.220359
Valle_del_Cauca	39.341767	5.950679	108.205629	117.730920	198.832574
Arauca	82.745985	15.884274	316.577271	79.421369	291.827356
Casanare	69.285665	15.456033	344.562941	160.422962	368.812923
Putumayo	56.840979	6.129910	114.517855	39.844412	194.485311
San_Andres	29.331871	5.101195	300.970502	137.732264	629.997577
Amazonas	83.724470	3.805658	258.784727	30.445262	318.406698
Guainia	85.163191	39.129034	135.800764	64.447820	202.550292
Guaviare	49.210474	5.180050	113.961098	18.130175	123.457856
Vaupes	0.000000	0.000000	4.451567	0.000000	2.225783
Vichada	15.528754	1.294063	38.821885	51.762514	78.937833

sns.heatmap(df2_pca.corr(), annot = True, cmap = "PuBu")
plt.show()

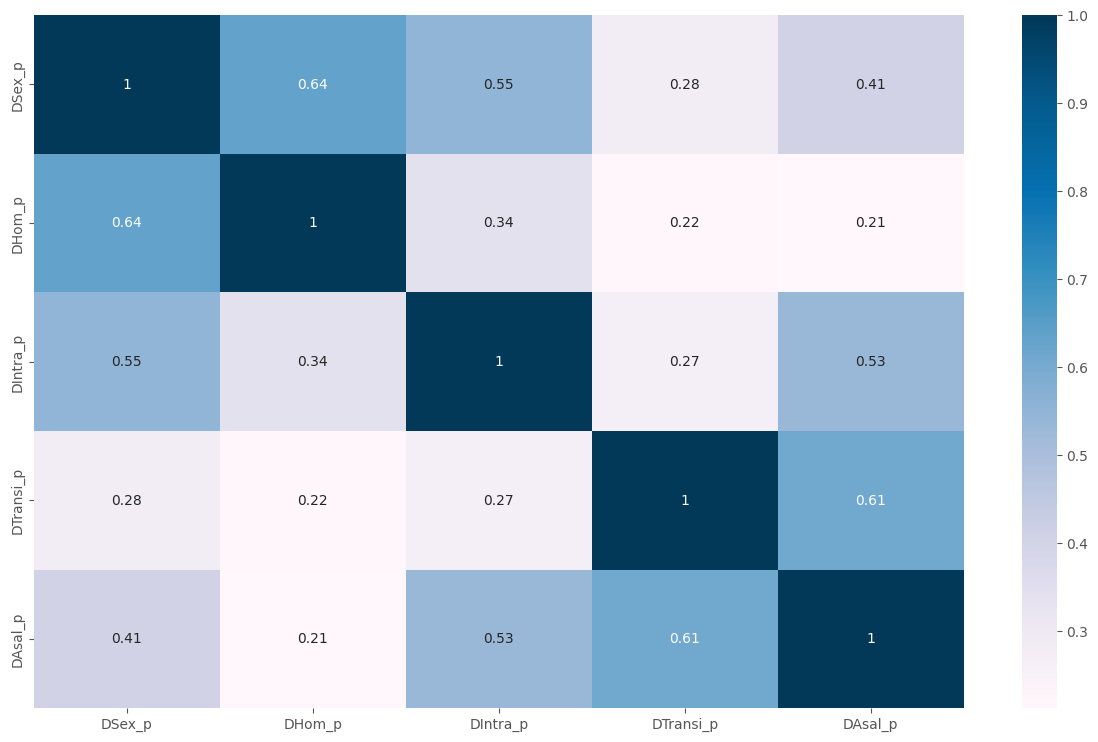
2. Vamos escalar la información para buscar mitigar la variables que tienen altas varianzas, ya que estas se llevarian el mayor de la variabilidad total. Deseamos que su variabilidad sea mitigada.

scaler2 = StandardScaler()            # Cargando el escalador estandar
scaler2.fit(df2_pca)                  # Calcula las medias y las desviaciones
X_scaled = scaler2.transform(df2_pca) # Estandariza la data.
pd.DataFrame(X_scaled, index = df2_pca.index, columns = df2_pca.columns)

	DSex_p	DHom_p	DIntra_p	DTransi_p	DAsal_p
Departamento
Antioquia	-0.663883	-0.196509	-0.199243	-0.104096	-0.361624
Atlantico	-0.239343	-0.508407	0.046727	-0.107368	-1.747823
Bogota_D.C.	0.281500	1.493371	1.195478	-1.285749	-1.503020
Bolivar	-0.113606	-0.790414	-0.509785	-0.693637	-0.379511
Boyaca	-0.268795	0.052035	0.833764	0.162437	0.750273
Caldas	-0.059184	-0.067750	-0.485429	0.771161	0.016557
Caqueta	-0.061174	-0.468669	-0.574400	-1.012212	-0.725149
Cauca	-0.795682	-0.365312	-0.414780	-0.370390	-0.439714
Cesar	0.339369	-0.399596	-0.094966	-0.049362	0.277503
Cordoba	-0.796998	-0.860150	-1.208040	-0.573843	-1.008305
Cundinamarca	0.308943	0.803913	-1.369223	0.172663	1.133231
Choco	-0.736138	-0.914445	-0.966477	-1.096403	-0.956544
Huila	-0.205885	-0.186039	0.520217	0.182038	0.751303
La_Guajira	-0.745839	-0.610629	-0.785435	-1.113233	-0.821455
Magdalena	-0.358869	-0.702906	0.025040	-0.505449	0.054491
Meta	1.751649	0.304650	1.547887	0.470162	1.159873
narigno	-1.717055	-0.382144	-0.662102	0.302682	-0.192256
Norte_de_Santander	-0.932852	-0.295230	0.201453	-0.087833	0.097127
Quindio	1.175131	0.971076	0.350610	2.288576	1.035139
Risaralda	0.495073	0.070287	0.053026	2.471654	0.071146
Santander	0.807637	0.263066	-1.408006	1.320347	1.057480
Sucre	0.014472	-0.701094	-0.189232	-0.897342	-0.245805
Tolima	-0.118026	-0.308773	0.130061	1.838545	0.605328
Valle_del_Cauca	-0.317508	-0.148872	-0.367528	0.633006	-0.195539
Arauca	1.825743	1.218310	2.063842	-0.042178	0.539031
Casanare	1.161088	1.159370	2.390391	1.385430	1.147144
Putumayo	0.546583	-0.124204	-0.293874	-0.739700	-0.229878
San_Andres	-0.811785	-0.265788	1.881736	0.985519	3.210255
Amazonas	1.874059	-0.444096	1.389494	-0.905355	0.748983
Guainia	1.945102	4.417535	-0.045536	-0.306079	-0.166173
Guaviare	0.169798	-0.254935	-0.300370	-1.122402	-0.790928
Vaupes	-2.260159	-0.967877	-1.578175	-1.441936	-1.748546
Vichada	-1.493367	-0.789772	-1.177127	-0.529650	-1.142594

# Realizamos la rutina habitual.
pca2 = PCA(n_components = 0.85) 
pca2.fit(X_scaled)
n_comp, var_exp = len(pca2.explained_variance_ratio_), sum(pca2.explained_variance_ratio_)
print("Con {} componentes se explica el {:.2f}% de la variabilidad".format(n_comp,var_exp*100))

Con 3 componentes se explica el 87.92% de la variabilidad

# Plot de sedimentación
sedimentacion(pca2)

pca2_trans = pca2.transform(X_scaled)
pca2_trans =  pd.DataFrame(pca2_trans, index = df2.index, columns = ["PC1","PC2","PC3"])
pca2_trans.head()

	PC1	PC2	PC3
Departamento
Antioquia	-0.712187	0.151438	-0.039164
Atlantico	-1.168391	-0.511234	0.088261
Bogota_D.C.	0.086747	-2.423493	0.615291
Bolivar	-1.062042	-0.059052	0.315585
Boyaca	0.694155	0.482570	0.583906

print("Se ajustó un PCA a una data de tamaño:",df2_pca.shape)
print("Se obtuvo un ajuste por PCA de tamaño:",pca2_trans.shape)
expl = pca2.explained_variance_ratio_
print("Cantidad de varianza explicada: {:.2f}%".format(sum(expl[0:3])*100))

Se ajustó un PCA a una data de tamaño: (33, 5)
Se obtuvo un ajuste por PCA de tamaño: (33, 3)
Cantidad de varianza explicada: 87.92%

# La correlación lineal debe ser 0.
pca2_trans.corr()

	PC1	PC2	PC3
PC1	1.000000e+00	-5.974580e-18	-2.520275e-18
PC2	-5.974580e-18	1.000000e+00	1.426259e-15
PC3	-2.520275e-18	1.426259e-15	1.000000e+00

## Plot loadings
plot_loadings_heatmap(pca2,df2_pca,n_compo=3)

view_index(df2_pca, ["Guainia","Arauca"])

	DSex_p	DHom_p	DIntra_p	DTransi_p	DAsal_p
Guainia	85.163191	39.129034	135.800764	64.447820	202.550292
Arauca	82.745985	15.884274	316.577271	79.421369	291.827356

df2_pca.mean()

DSex_p        45.771800
DHom_p         7.032346
DIntra_p     139.703236
DTransi_p     81.814546
DAsal_p      223.587321
dtype: float64

fig = px.scatter(
    pca2_trans,
    x="PC1",
    y="PC2",
    text=pca2_trans.index,
    hover_name=pca2_trans.index,
    title="Interpretación"
)

fig.add_hline(y=0, line_color="yellow")
fig.add_vline(x=0, line_color="yellow")

biplot(pca2, df2_pca, 1, 2)

biplot(pca2,df2_pca, 1, 3)

biplot(pca2, df2_pca, 2, 3)

Ejemplo 3.

El siguiente dataframe contiene los cambios de indices bursatiles para las 517 empresas más importantes de los EEUU. Este dataframe es muy usado en series de tiempo pues muestra el comportamiento de las empresas a través de la historia.

df_path3 = "sp500_data.csv.gz"
sp500_px = pd.read_csv(url_base+df_path3, compression='gzip', index_col=0)
sp500_px.head()

	ADS	CA	MSFT	RHT	CTSH	CSC	EMC	IBM	XRX	ALTR	...	WAT	ALXN	AMGN	BXLT	BIIB	CELG	GILD	REGN	VRTX	HSIC
1993-01-29	0.0	0.060124	-0.022100	0.0	0.0	0.018897	0.007368	0.092165	0.259140	-0.007105	...	0.0	0.0	0.34716	0.0	0.04167	0.00000	0.015564	1.75	0.1250	0.0
1993-02-01	0.0	-0.180389	0.027621	0.0	0.0	0.018889	0.018425	0.115207	-0.100775	0.063893	...	0.0	0.0	-0.23144	0.0	0.00000	-0.01041	0.007782	1.25	0.1250	0.0
1993-02-02	0.0	-0.120257	0.035900	0.0	0.0	-0.075573	0.029482	-0.023041	0.028796	-0.014192	...	0.0	0.0	-0.11572	0.0	0.00000	0.00000	-0.007792	-0.25	0.0000	0.0
1993-02-03	0.0	0.060124	-0.024857	0.0	0.0	-0.151128	0.003689	-0.253454	-0.043190	-0.007105	...	0.0	0.0	-0.08679	0.0	0.04167	-0.04167	-0.038919	-0.50	0.0625	0.0
1993-02-04	0.0	-0.360770	-0.060757	0.0	0.0	0.113350	-0.022114	0.069862	0.000000	-0.007096	...	0.0	0.0	0.14465	0.0	-0.04166	-0.03126	-0.046711	0.00	0.0625	0.0

5 rows × 517 columns

Para muestro análisis vamos a considerar las siguientes empresas:

Eitiqueta	Nombre	Sector
AAPL	Apple Inc.	Information Technology
MSFT	Microsoft Corp	Information Technology
CSCO	Cisco Systems	Information Technology
INTC	Intel Corp	Information Technology
CVX	Chevron Corp.	Energy
XOM	Exxon Mobil Corp	Energy
SLB	Schlumberger Ltd	Energy
COP	ConocoPhillips	Energy
JPM	JPMorgan Chase & Co	Financials
WFC	Wells Fargo	Financials
USB	U.S. Bancorp	Financials
AXP	American Express Co	Financials
WMT	Wal-Mart Stores	Consumer Staples
TGT	Target Corp.	Consumer Discretionary
HD	Home Depot	Consumer Discretionary
COST	Costco Wholesale Corp.	Consumer Staples

Además de considerar los datos desde el 01 de enero de 2011 y hasta el final de los registros, en este caso 01 de julio del año 2015.

col_sel = sorted(["AAPL", "MSFT", "CSCO", "INTC", "CVX", "XOM", "SLB", "COP", "JPM", "WFC", 
                  "USB", "AXP", "WMT", "TGT", "HD", "COST"])
df_pca3 = sp500_px.loc[sp500_px.index >= "2011-01-01", col_sel]
df_pca3.head()

	AAPL	AXP	COP	COST	CSCO	CVX	HD	INTC	JPM	MSFT	SLB	TGT	USB	WFC	WMT	XOM
2011-01-03	0.527368	0.093870	-0.336272	-0.240605	0.035704	0.240681	0.099184	-0.137211	0.512093	-0.061805	-0.325923	0.455646	-0.234866	0.250042	0.294839	0.736805
2011-01-04	-0.154321	-0.431788	-0.463161	-0.171859	0.008926	-0.584516	-0.541005	0.025726	0.335894	0.132440	-2.030049	-0.580720	-0.153566	0.000000	0.142951	0.168668
2011-01-05	0.597152	0.895406	-0.057104	-0.859307	0.169599	0.446985	-0.054099	-0.214392	0.689468	0.088294	1.536499	-0.482448	0.198732	0.857284	-0.303772	0.026631
2011-01-06	-0.132850	-0.612646	-0.463161	0.249200	0.035706	-0.919751	-0.189354	0.085757	0.070713	0.688689	-1.927614	-0.786210	-0.532962	0.000000	-0.312709	0.248558
2011-01-07	0.285820	-0.537242	-0.006350	-0.257788	0.098187	0.180511	-0.036064	-0.042878	-0.795539	-0.035317	0.931215	-0.089345	-0.171633	-0.651894	0.169758	0.337329

Realizamos la rutina habitual.

scaler3 = StandardScaler()
scaler3.fit(df_pca3)
X_scaled3 = scaler3.transform(df_pca3)
pd.DataFrame(X_scaled3, index=df_pca3.index, columns=df_pca3.columns)

	AAPL	AXP	COP	COST	CSCO	CVX	HD	INTC	JPM	MSFT	SLB	TGT	USB	WFC	WMT	XOM
2011-01-03	0.561707	0.110812	-0.509688	-0.299786	0.117204	0.252913	0.094034	-0.555764	0.920070	-0.213019	-0.267647	0.794378	-0.764788	0.630204	0.509947	0.985516
2011-01-04	-0.107735	-0.651798	-0.710903	-0.220968	-0.008461	-0.599033	-0.824095	0.021865	0.596087	0.317332	-1.805599	-1.045530	-0.513618	-0.026284	0.212894	0.193236
2011-01-05	0.630238	1.273658	-0.066998	-1.009130	0.745557	0.465905	-0.125796	-0.829379	1.246217	0.196799	1.413166	-0.871062	0.574786	2.224522	-0.660779	-0.004839
2011-01-06	-0.086650	-0.914182	-0.710904	0.261778	0.117213	-0.945136	-0.319773	0.234680	0.108487	1.836075	-1.713152	-1.410346	-1.685740	-0.026284	-0.678256	0.304644
2011-01-07	0.324498	-0.804788	0.013486	-0.319486	0.410429	0.190793	-0.099932	-0.221342	-1.484324	-0.140698	0.866905	-0.173168	-0.569436	-1.737836	0.265322	0.428437
...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...
2015-06-25	-1.291754	-1.629728	-1.482904	-1.170435	-0.795464	-1.141553	-1.482363	-0.175690	-1.245487	-1.081788	-0.596224	0.127481	-0.776401	-1.549084	-1.220558	-1.324935
2015-06-26	-0.859656	-0.444529	0.071124	0.113645	-1.028313	0.376100	-0.292015	-1.806437	-0.003276	-1.109110	0.279190	-0.742435	-0.100977	0.236264	0.246246	-0.000142
2015-06-29	-0.869479	-2.077787	-0.626603	-1.537309	-2.145990	-0.831825	-1.511042	-1.168325	-0.898404	-1.873597	0.080650	-2.482293	-1.583905	-1.969155	-0.809870	-0.362721
2015-06-30	-0.093671	-0.678215	-0.166733	-1.537325	-1.773440	-1.007334	-0.076901	-0.813805	-0.259013	-1.573247	-0.144973	-1.825412	-1.398532	-0.813934	-1.787726	-0.795020
2015-07-01	-0.250801	-0.373553	-2.323355	0.778636	-0.378852	-0.212384	-0.593184	-1.168318	-0.113478	-0.071570	-1.886774	1.565507	0.671398	-0.498876	0.480924	-1.310987

1131 rows × 16 columns

## Realizamos la rutina habitual.
pca3 = PCA() 
pca3.fit(X_scaled3)

PCA()

In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.

## Plot de sedimentación.
sedimentacion(pca3)

Como se ve en el plot anterior, la varianza del primer componente principal es bastante grande (como suele ser el caso), pero los otros componentes principales también son significativos.

¿Cuántas compomentes principales de deben seleccionar?

## Plot loadings
plot_loadings_heatmap(pca3, df_pca3, n_compo=5)

En el heatmap anterior se muestran las cargas para las primeras 5 compomentes principales del objeto pca3.

• Los loadings del primer componente principal tienen el mismo signo, esto sucede típicamente cuando las features comparten un factor común (aquí, la tendencia general del mercado de valores).

plot_loadings_bar(pca3, df_pca3, n_compo=6)

• Al parecer el segundo componente captura los cambios de precio en aquellas acciones del sector de energía en comparación con las otras acciones.

• El tercer componente es principalmente un contraste en los movimientos de Apple y Cost.

• El cuarto componente contrasta los movimientos de Schlumberger (SLB) al resto de acciones energéticas.

• El quinto componente está mayoritariamente dominado por empresas financieras.

biplot(pca3, df_pca3, 1, 5)

biplot1(pca3,df_pca3)

Conclusiones.

1. PCA es una técnica lineal que busca reducir la dimensionalidad del dataset buscando optimizar la perdida de información presente en la variabilidad.

2. Una desventaja de PCA es que los dos ejes del primer plano factorial a menudo no son muy fáciles de interpretar. Esto debido a que las componentes principales corresponden a direcciones en los datos originales, dado que son combinaciones de las features originales.

3. Existen técnicas más modernas para realizar la reducción de dimensionalidad en el dataset, algunas las desarrollaremos más adelante en el curso.

Tarea 2

Realizar un análisis de compomentes principales de la tabla de los resultados de las pruebas ICFES 2019-2.