Random Forrest

Universidad Central

Maestría en analítica de datos

Métodos estadísticos para analítica de datos.

Docente: Luis Andrés Campos Maldonado.

import warnings
warnings.filterwarnings("ignore")

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from pprint import pprint
from sklearn.compose import ColumnTransformer
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import OneHotEncoder, label_binarize
from sklearn.ensemble import RandomForestClassifier
from sklearn.metrics import roc_curve, auc
    
plt.style.use("ggplot")
plt.rcParams["figure.figsize"] = (15,6)

url_base = "https://raw.githubusercontent.com/lacamposm/Metodos-Estadisticos/main/data/"

Bagging y Random Forrest

Supongamos que hace una pregunta compleja a miles de personas al azar y luego agrega las respuestas, en muchos casos se encontrará que la respuesta agregada es mejor que la respuesta de un experto esto es llamado sabiduría de la multitud (wisdom of the crowd). Ahora, pensando en el machine learning, si agregamos las predicciones de un grupo de predictores (clasificador o regresores) a menudo se obtiene mejores predicciones que con el mejor predictor original. Un grupo de predictores se denomina ensemble; luego, esta técnica se denomina Ensemble Learning.

Por ejemplo, puede entrenar un grupo de clasificadores DecisionTree, cada uno en un subconjunto aleatorio del set de train. Para hacer predicciones, solo se obtienen las predicciones de todos los árboles individuales, luego se predice la clase que obtiene la mayor cantidad de votos. Tal conjunto de árboles de decisión se llama Random Forest, y a pesar de su sencillez, es uno de los más potentes algoritmos de Machine Learning disponibles en la actualidad.

NOTA:

Los metodos de ensamble funcionan mejor cuando los predictores son lo más independientes posible entre sí. Una forma de obtener clasificadores diversos es entrenarlos usando algoritmos muy diferentes. Esto aumenta la posibilidad de que cometan muy diferentes tipos de errores, mejorando la precisión del conjunto.

Bagging y pasting.

Una forma de obtener un conjunto diverso de clasificadores es usar algoritmos de entrenamiento muy diferentes. Otro enfoque es usar el mismo algoritmo de entrenamiento para todo predictor y entrenarlos en diferentes subconjuntos aleatorios del set de train. Cuando el muestreo se realiza con reemplazo, este método se llama bagging (bootstrap-aggregating). Cuando el muestreo se realiza sin reposición, es llamado pasting.

Tanto en bagging como en pasting se permiten muestrear registros del set de train varias veces a través de múltiples predictores, pero solo el bagging permite a los registro del set de train muestrearse varias veces para el mismo predictor.

Una vez que se entrenan todos los predictores, el ensemble puede hacer una predicción para un nuevo registro simplemente agregando las predicciones de todos los predictores. La aggregation function es normalmente la MODA estadística (es decir, la predicción más frecuente) para la clasificación, o el promedio para la regresión. Cada predictor individual tiene un mayor sesgo que si se entrenara en el set de train original, pero la agregación reduce tanto el sesgo como la varianza. Generalmente, el resultado neto es que el conjunto tiene un sesgo similar pero una varianza menor que un solo predictor entrenado en el set de train original.

Algoritmo Bagging

Supongamos que tenemos una variable respuesta \(Y\) y \(p\) variables predictoras \(\mathbf{X} = (X_1, X_2, \ldots, X_p)\) con \(n\) registros. El Bagging se forma del algoritmo básico para ensembles, excepto que, en lugar de ajustar varios modelos a la misma data, cada nuevo modelo se ajusta a un remuestreo bootstrap.

Algoritmo:

1. Inicialización:

   • Inicialice \(M\), el número de modelos a ajustar.

   • Establezca la iteración \(m = 1\).

2. Generación de Submuestras Bootstrap:

   • Tome una nueva remuestra de bootstrap (es decir, con reemplazo) de \(n\) registros del conjunto de entrenamiento para formar una submuestra \(Y_m\) y \(\mathbf{X}_m\) (el “bag”).

3. Entrenamiento del Modelo:

   • Entrene un modelo usando \(Y_m\) y \(\mathbf{X}_m\) para crear un conjunto de reglas de decisión \(\hat{f}_m(\mathbf{X})\).

4. Incremento del Contador:

   • Incrementa el contador del modelo \(m = m + 1\).

   • Si \(m \leq M\), vuelve al paso 2.

5. Combinación de Predicciones:

   • Para Clasificación:

     • Si \(\hat{f}_m\) predice la probabilidad de que \(Y = 1\), la estimación bagged viene dada por la votación mayoritaria:

     \[\hat{f}=\frac{1}{M}\left(\hat{f_1}(\mathbf{X})+\hat{f_2}(\mathbf{X})+\cdots+ \hat{f_M}(\mathbf{X})\right)\]

     • Si \(\hat{f}_m\) predice la clase de la instancia, la estimación bagged viene dada por la votación mayoritaria:

     \[\hat{f}= moda\left(\hat{f_1}(\mathbf{X}), \hat{f_2}(\mathbf{X}), \cdots, \hat{f_M}(\mathbf{X})\right)\]

   • Para Regresión:

     • Si \(\hat{f}_m\) predice un valor continuo, la estimación bagged viene dada por el promedio de las predicciones:

     \[\hat{f}=\frac{1}{M}\left(\hat{f_1}(\mathbf{X})+\hat{f_2}(\mathbf{X})+\cdots+\hat{f_M}(\mathbf{X})\right)\]

Notas Adicionales:

• Tamaño de la Submuestra: En el paso 2, se menciona que se toma una remuestra de \(n\) registros. Esto es típico en el bagging, donde el tamaño de la submuestra es igual al tamaño del conjunto de datos original. Sin embargo, en algunas variantes, el tamaño de la submuestra puede ser menor que \(n\).

• Modelos Base: Los modelos base utilizados en el bagging pueden ser de cualquier tipo, pero los árboles de decisión son comúnmente utilizados debido a su alta varianza y baja capacidad de generalización individual, lo que se compensa al combinarlos en un ensemble.

NOTA:

1. En Scikit-Learn, puede establecer oob_score=True al crear un BaggingClassifier para solicitar una evaluación oob automática después del entrenamiento.

2. La función de decisión oob para cada registro del set de train también está disponible a través del atributo oob_decision_function_. En este caso que el estimador base tenga un método como predict_proba(), la función de decisión devuelve las probabilidades de clase para cada registro del set de train.

Random Forrest.

Random Forrest es un ensemble basado en bagging de DecisionTrees, con una importante extensión: además de muestrear los registros del set de train también muestrea las features. En los DecisionTree tradicionales, para determinar cómo crear una subpartición de un partición \(A\), el algoritmo elige la variable y el punto de división minimizando un criterio como la impureza de Gini. Con Random Forrest, en cada etapa del algoritmo, la elección de la feature es limitada a un subconjunto aleatorio de features.

NOTA:

1. Generalmente se entrena con max_samples ajustado al tamaño del set de train.

2. Una regla empírica es elegir \(\sqrt{P}\) donde \(P\) es el número de variables predictoras.

Algoritmo Random Forrest.

En comparación con el algoritmo de DecisionTree, el algoritmo de Random Forrest agrega dos pasos más: el bagging y el bootstrap sampling de features en cada división:

1. Tome una submuestra de bootstrap (con reemplazo) de los registros.

2. Para la primera división, muestree \(p< P\) variables al azar sin reemplazo.

3. Para cada una de las variables muestreadas \(X_{j(1)}, X_{j(2)},⋯,X_{j(p)}\), aplicar el siguiente algortimo de división:

   • A) Para cada valor \(s_{j(k)}\) de \(X_{j(k)}\):

     • Divida los registros en la partición \(A\), con \(X_{j(k)}< s_{j(k)}\) como una partición y los registros restantes donde \(X_{j(k)}≥ s_{j(k)}\) como otra partición.

     • Mida la homogeneidad de las clases dentro de cada subpartición de A.

   • B) Seleccione el valor de \(s_{j(k)}\) que produce la máxima homogeneidad dentro de la partición de clase.

4. Seleccione la variable \(X_{j(k)}\) y el valor de división \(s_{j(k)}\) que produce la máxima homogeneidad de clase dentro de la partición.

5. Seleccione un nuevo subconjunto de \(p\) variables al azar para la siguiente división del árbol, y repita el proceso desde el paso 3 para determinar la mejor división en este nodo.

6. Continúe con divisiones adicionales, siguiendo el mismo procedimiento hasta que el árbol logre su máximo crecimiento.

7. Vuelva al paso 1, tome otra submuestra de arranque y comience el proceso de nuevo otra vez.

Nuevo modelo de incumplimiento de pago.

Problema: Construir un modelo de clasificación para determinar si un usuario pagará su préstamo o no.

Nuestra data de trabajo.

# Preparamos la Data
df_prestamos = pd.read_parquet(url_base + "Logistic_Regression_1.parquet",)
df_prestamos.drop_duplicates(inplace=True)
df_prestamos["tasa_de_interes"] = df_prestamos["tasa_de_interes"].str.replace("%", "").astype("float")
df_prestamos

	estado_del_prestamo	ingreso_anual	estado_de_verificacion	anios_de_experiencia_laboral	tenencia_de_vivienda	tasa_de_interes	monto_del_prestamo	proposito	plazo	calificacion
0	completamente_pagado	24000.0	verificado	10+ años	alquiler	10.65	5000	tarjeta_de_credito	36 meses	B
1	dado_de_baja	30000.0	verificado_con_fuente	< 1 año	alquiler	15.27	2500	auto	60 meses	C
2	completamente_pagado	12252.0	no_verificado	10+ años	alquiler	15.96	2400	pequeno_negocio	36 meses	C
3	completamente_pagado	49200.0	verificado_con_fuente	10+ años	alquiler	13.49	10000	otro	36 meses	C
4	completamente_pagado	80000.0	verificado_con_fuente	1 año	alquiler	12.69	3000	otro	60 meses	B
...	...	...	...	...	...	...	...	...	...	...
38700	completamente_pagado	110000.0	no_verificado	4 años	hipoteca	8.07	2500	remodelacion_del_hogar	36 meses	A
38701	completamente_pagado	18000.0	no_verificado	3 años	alquiler	10.28	8500	tarjeta_de_credito	36 meses	C
38702	completamente_pagado	100000.0	no_verificado	< 1 año	hipoteca	8.07	5000	consolidacion_de_deudas	36 meses	A
38703	completamente_pagado	200000.0	no_verificado	< 1 año	hipoteca	7.43	5000	otro	36 meses	A
38704	completamente_pagado	22000.0	no_verificado	< 1 año	propia	13.75	7500	consolidacion_de_deudas	36 meses	E

38689 rows × 10 columns

Random Forrest buscando mejorar Decisicion Tree

Vamos a ajustar un clasificador Random Forrest con las covariables plazo y ingreso_anual y generemos la curva ROC asociada.

df_rf1 = df_prestamos.copy()[["estado_del_prestamo", "ingreso_anual", "plazo"]]
df_rf1

	estado_del_prestamo	ingreso_anual	plazo
0	completamente_pagado	24000.0	36 meses
1	dado_de_baja	30000.0	60 meses
2	completamente_pagado	12252.0	36 meses
3	completamente_pagado	49200.0	36 meses
4	completamente_pagado	80000.0	60 meses
...	...	...	...
38700	completamente_pagado	110000.0	36 meses
38701	completamente_pagado	18000.0	36 meses
38702	completamente_pagado	100000.0	36 meses
38703	completamente_pagado	200000.0	36 meses
38704	completamente_pagado	22000.0	36 meses

38689 rows × 3 columns

categorical_features = ["plazo"]
numeric_features = ["ingreso_anual"]

preprocessor = ColumnTransformer(
    transformers=[
        ("onehot", OneHotEncoder(), categorical_features),
        ("num", "passthrough", numeric_features)        
    ]
)

clf_rf1 = RandomForestClassifier(
    n_estimators=100,
    max_depth=2,
    random_state=42
)



X = df_rf1[categorical_features + numeric_features]
y = label_binarize(df_rf1["estado_del_prestamo"], classes=["dado_de_baja", "completamente_pagado"])
clf_rf1.fit(preprocessor.fit_transform(X), y)

RandomForestClassifier(max_depth=2, random_state=42)

In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.

# Curva de ROC RandomForestClassifier
probas1 = clf_rf1.predict_proba(preprocessor.fit_transform(X))[:,1]
fpr, tpr, _ = roc_curve(y, probas1)
#
plt.plot(fpr,tpr, label=f"Random Forrest  (AUC = {auc(fpr, tpr):.2f})", color="blue")
plt.plot((0,1), (0,1), ls = "--", color="grey", label="Randow guess")
plt.legend(loc="lower right")
plt.title("Receiver operating characteristic")
plt.show()

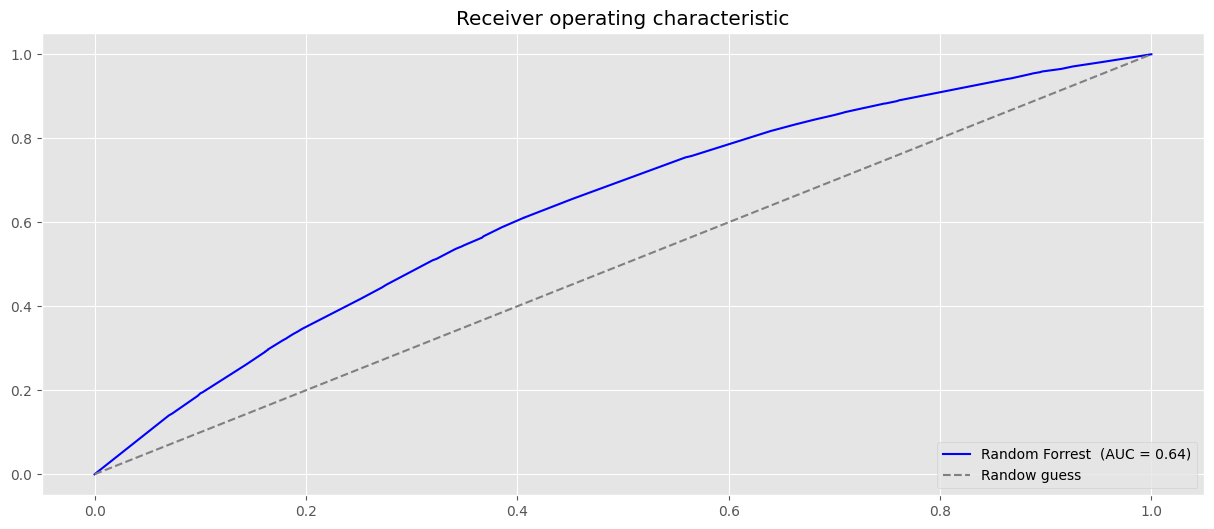
Podemos ver que hay un aumento en AUC usando el algoritmo de bosque aleatorio. Con solo dos covariables, podemos lograr un aumento bastante significativo en el rendimiento. Esta diferencia probablemente sería más pronunciada con más variables.

Modelo con todas las covariables

df_full = df_prestamos.copy()
df_full.drop(columns=["estado_de_verificacion"], inplace=True)
df_full

	estado_del_prestamo	ingreso_anual	anios_de_experiencia_laboral	tenencia_de_vivienda	tasa_de_interes	monto_del_prestamo	proposito	plazo	calificacion
0	completamente_pagado	24000.0	10+ años	alquiler	10.65	5000	tarjeta_de_credito	36 meses	B
1	dado_de_baja	30000.0	< 1 año	alquiler	15.27	2500	auto	60 meses	C
2	completamente_pagado	12252.0	10+ años	alquiler	15.96	2400	pequeno_negocio	36 meses	C
3	completamente_pagado	49200.0	10+ años	alquiler	13.49	10000	otro	36 meses	C
4	completamente_pagado	80000.0	1 año	alquiler	12.69	3000	otro	60 meses	B
...	...	...	...	...	...	...	...	...	...
38700	completamente_pagado	110000.0	4 años	hipoteca	8.07	2500	remodelacion_del_hogar	36 meses	A
38701	completamente_pagado	18000.0	3 años	alquiler	10.28	8500	tarjeta_de_credito	36 meses	C
38702	completamente_pagado	100000.0	< 1 año	hipoteca	8.07	5000	consolidacion_de_deudas	36 meses	A
38703	completamente_pagado	200000.0	< 1 año	hipoteca	7.43	5000	otro	36 meses	A
38704	completamente_pagado	22000.0	< 1 año	propia	13.75	7500	consolidacion_de_deudas	36 meses	E

38689 rows × 9 columns

categorical_features = [col for col in df_full.select_dtypes(exclude=np.number).columns if col != "estado_del_prestamo"]
numeric_features = [col for col in df_full.columns if col not in categorical_features and col != "estado_del_prestamo"]

preprocessor = ColumnTransformer(
    transformers=[
        ("onehot", OneHotEncoder(sparse_output=False), categorical_features),
        ("num", "passthrough", numeric_features)        
    ]
)

clf_rf_full = RandomForestClassifier(
    n_estimators=100,
    max_depth=3,
    random_state=123,
    oob_score=True
)

X = df_full[categorical_features + numeric_features]
y = label_binarize(df_full["estado_del_prestamo"], classes=["dado_de_baja", "completamente_pagado"])
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, stratify=y, random_state=123)
clf_rf_full.fit(preprocessor.fit_transform(X_train), y_train)

RandomForestClassifier(max_depth=3, oob_score=True, random_state=123)

In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.

# AUC en train.
fpr, tpr, _ = roc_curve(y_train, clf_rf_full.predict_proba(preprocessor.fit_transform(X_train))[:, 1])
plt.plot(fpr, tpr, label=f"RandomForestClassifier (AUC Train={auc(fpr, tpr):.4f})")

# AUC en test.
fpr, tpr, _ = roc_curve(y_test, clf_rf_full.predict_proba(preprocessor.fit_transform(X_test))[:, 1])
plt.plot(fpr, tpr, label=f"RandomForestClassifier (AUC Test={auc(fpr, tpr):.4f})")

plt.xlabel("False Positive Rate")
plt.ylabel("True Positive Rate")
plt.title("Receiver operating characteristic")
plt.plot((0,1), (0,1), ls="--", color="grey", label="Randow guess")
plt.legend(loc="lower right")
plt.show()

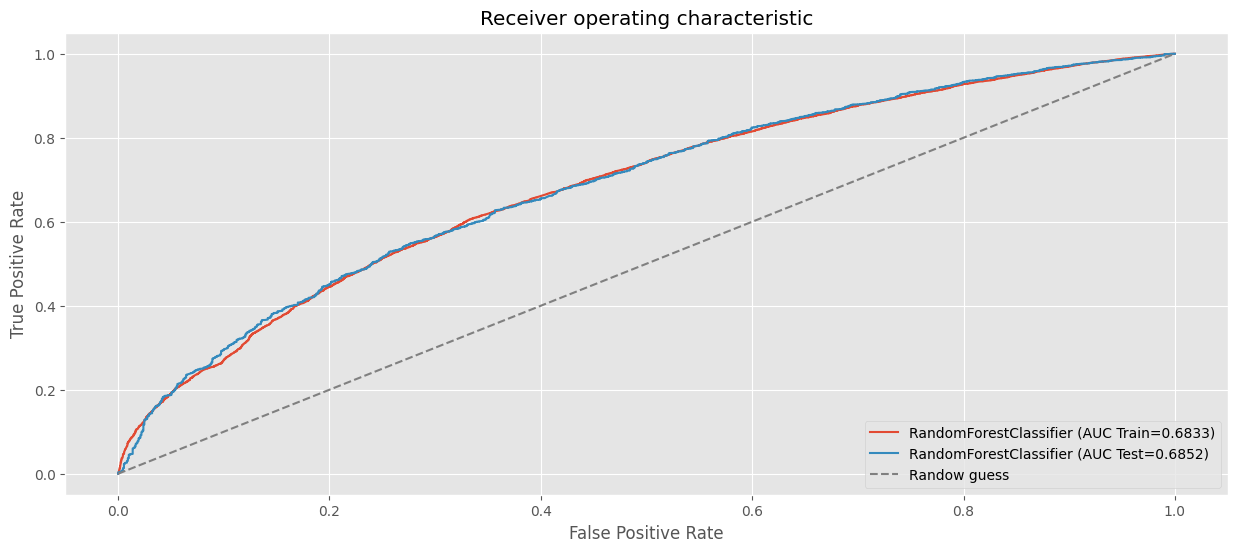
clf_rf_full2 = RandomForestClassifier(
    n_estimators=100,
    max_depth=3,
    random_state=123,
    oob_score=True,
    min_samples_leaf=300
)

clf_rf_full2.fit(preprocessor.fit_transform(X_train), y_train)

# AUC en train.
fpr, tpr, _ = roc_curve(y_train, clf_rf_full2.predict_proba(preprocessor.fit_transform(X_train))[:, 1])
plt.plot(fpr, tpr, label=f"RandomForestClassifier (AUC Train={auc(fpr, tpr):.4f})")

# AUC en test.
fpr, tpr, _ = roc_curve(y_test, clf_rf_full2.predict_proba(preprocessor.fit_transform(X_test))[:, 1])
plt.plot(fpr, tpr, label=f"RandomForestClassifier (AUC Test={auc(fpr, tpr):.4f})")

plt.xlabel("False Positive Rate")
plt.ylabel("True Positive Rate")
plt.title("Receiver operating characteristic")
plt.plot((0,1), (0,1), ls="--", color="grey", label="Randow guess")
plt.legend(loc="lower right")
plt.show()

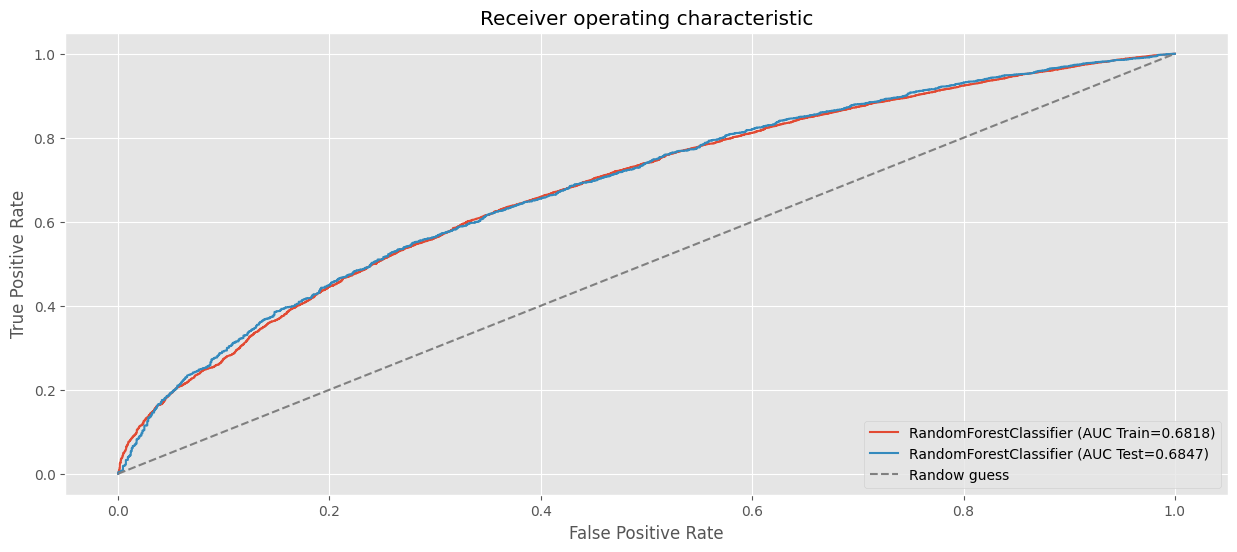
clf_rf_full3 = RandomForestClassifier(
    n_estimators=90,
    criterion="gini",
    max_depth=6,
    random_state=42,
    min_samples_leaf=5,
    min_samples_split=700,
    oob_score=True
)

clf_rf_full3.fit(preprocessor.fit_transform(X_train), y_train)

# AUC en train.
fpr, tpr, _ = roc_curve(y_train, clf_rf_full3.predict_proba(preprocessor.fit_transform(X_train))[:, 1])
plt.plot(fpr, tpr, label=f"RandomForestClassifier (AUC Train={auc(fpr, tpr):.4f})")

# AUC en test.
fpr, tpr, _ = roc_curve(y_test, clf_rf_full3.predict_proba(preprocessor.fit_transform(X_test))[:, 1])
plt.plot(fpr, tpr, label=f"RandomForestClassifier (AUC Test={auc(fpr, tpr):.4f})")

plt.xlabel("False Positive Rate")
plt.ylabel("True Positive Rate")
plt.title("Receiver operating characteristic")
plt.plot((0,1), (0,1), ls="--", color="grey", label="Randow guess")
plt.legend(loc="lower right")
plt.show()

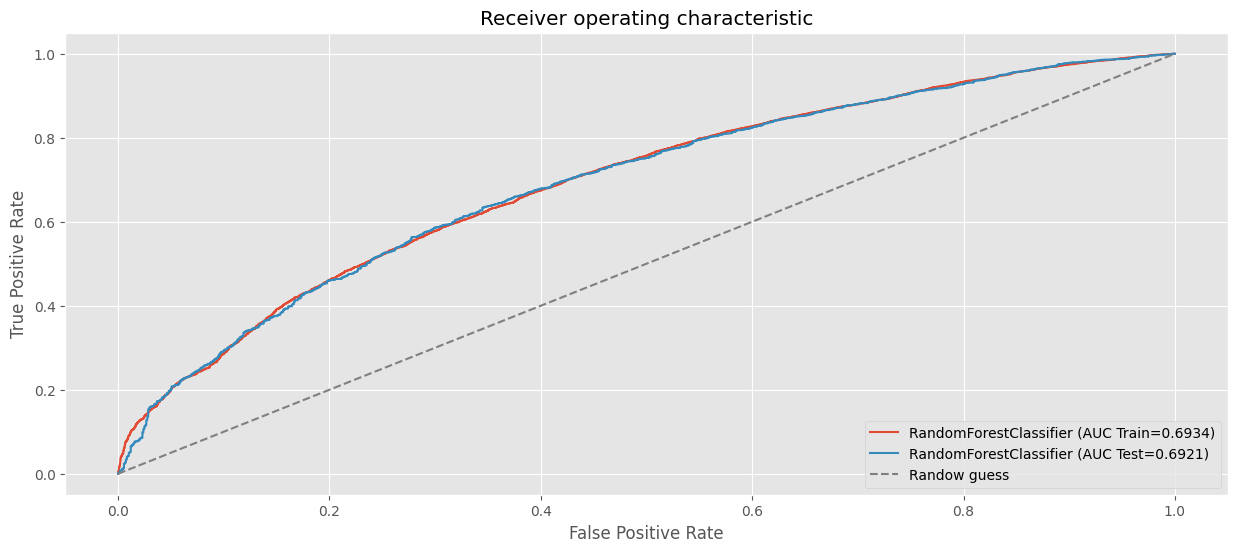
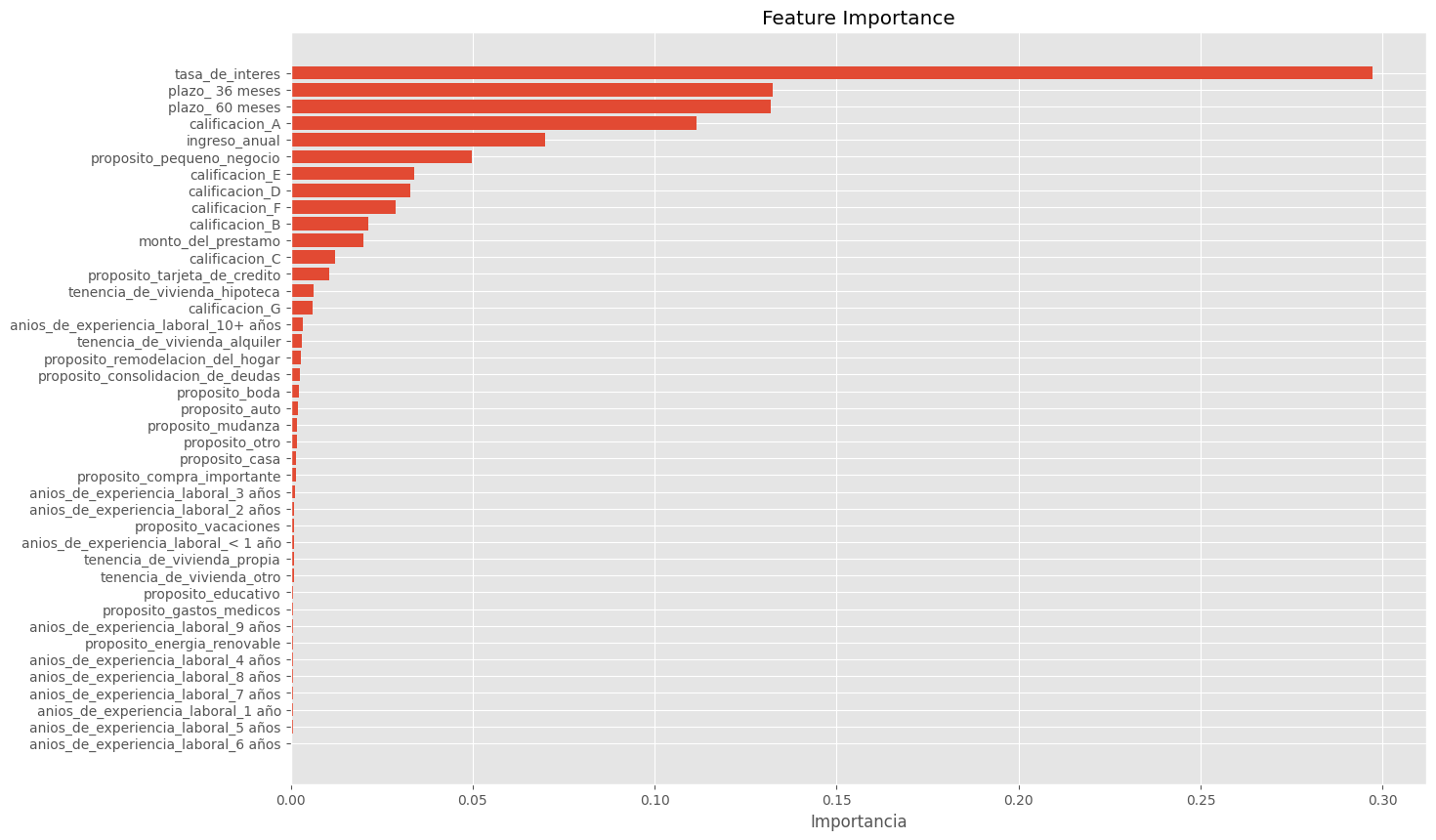
Feature Importance en Random Forest

La feature importance mide la relevancia de cada característica para las predicciones del modelo. En Random Forest, se calcula mediante:

• Reducción Promedio de la Impureza (MDI):

  • Calcula cuánto reduce la impureza (Gini o entropía) al usar una característica para dividir un nodo.

  • Predeterminado en scikit-learn.

Impacto de las Variables Categóricas

• Las variables categóricas con muchas categorías o pocas observaciones en ciertas categorías pueden sesgar la importancia.

• Categorías poco representadas:

  • Contribuyen menos al modelo por la falta de información estadística.

  • Pueden aumentar el riesgo de sobreajuste si capturan ruido en lugar de patrones reales.

Interpretación

• Valores más altos indican mayor relevancia de una característica.

• Ayuda a identificar las variables clave y eliminar las irrelevantes.

Ventajas y Limitaciones

• Ventajas: Intuitivo, útil para simplificar modelos.

• Limitaciones:

  1. Sesgo hacia variables categóricas con muchas categorías.

  2. Poca utilidad de categorías infrecuentes.

  3. Dificultad para capturar interacciones.

  4. Dependencia del método (MDI puede sobrestimar).

encoded_categorical_names = preprocessor.named_transformers_["onehot"].get_feature_names_out(categorical_features)
numeric_names = numeric_features
transformed_feature_names = list(encoded_categorical_names) + numeric_names
importances = clf_rf_full3.feature_importances_
importance_df = pd.DataFrame({"Feature": transformed_feature_names, "Importance": importances})
importance_df = importance_df.sort_values(by="Importance", ascending=False).reset_index(drop=True)
importance_df

	Feature	Importance
0	tasa_de_interes	0.297144
1	plazo_ 36 meses	0.132306
2	plazo_ 60 meses	0.131824
3	calificacion_A	0.111486
4	ingreso_anual	0.070003
5	proposito_pequeno_negocio	0.049825
6	calificacion_E	0.033946
7	calificacion_D	0.032778
8	calificacion_F	0.028853
9	calificacion_B	0.021430
10	monto_del_prestamo	0.019959
11	calificacion_C	0.012219
12	proposito_tarjeta_de_credito	0.010679
13	tenencia_de_vivienda_hipoteca	0.006361
14	calificacion_G	0.006122
15	anios_de_experiencia_laboral_10+ años	0.003412
16	tenencia_de_vivienda_alquiler	0.002975
17	proposito_remodelacion_del_hogar	0.002744
18	proposito_consolidacion_de_deudas	0.002609
19	proposito_boda	0.002207
20	proposito_auto	0.001956
21	proposito_mudanza	0.001829
22	proposito_otro	0.001725
23	proposito_casa	0.001575
24	proposito_compra_importante	0.001543
25	anios_de_experiencia_laboral_3 años	0.001228
26	anios_de_experiencia_laboral_2 años	0.001032
27	proposito_vacaciones	0.000919
28	anios_de_experiencia_laboral_< 1 año	0.000915
29	tenencia_de_vivienda_propia	0.000871
30	tenencia_de_vivienda_otro	0.000818
31	proposito_educativo	0.000775
32	proposito_gastos_medicos	0.000752
33	anios_de_experiencia_laboral_9 años	0.000717
34	proposito_energia_renovable	0.000716
35	anios_de_experiencia_laboral_4 años	0.000697
36	anios_de_experiencia_laboral_8 años	0.000679
37	anios_de_experiencia_laboral_7 años	0.000678
38	anios_de_experiencia_laboral_1 año	0.000643
39	anios_de_experiencia_laboral_5 años	0.000554
40	anios_de_experiencia_laboral_6 años	0.000496

plt.figure(figsize=(15, 10))
plt.barh(importance_df["Feature"], importance_df["Importance"])
plt.xlabel("Importancia")
plt.ylabel("")
plt.title("Feature Importance")
plt.gca().invert_yaxis()
plt.show()

Out-of-Bag (OOB) en Random Forest

Out-of-Bag Evaluation

Con bagging, algunas instancias se pueden muestrear varias veces para cualquier predictor dado, mientras que otros pueden no ser muestreados en absoluto. Por defecto, un BaggingClassifier toma \(m\) registros del set de train con reemplazo (bootstrap=True), donde \(m\) es el tamaño del conjunto de entrenamiento. Esto significa que solo alrededor del \(63\%\) de los registros del set de entrenamiento se muestrean en promedio para cada predictor. El \(37\%\) restante de los registros que no son muestreados se denominan registros (instancias) out-of-bag (oob).

El Out-of-Bag (OOB) es una técnica útil para evaluar el rendimiento de un modelo de Random Forest durante el entrenamiento, sin necesidad de un conjunto de validación separado.

¿Cómo Funciona el OOB?

1. Selección de Datos por Bootstrap:

   • Cada árbol se entrena con un subconjunto de los datos seleccionados mediante muestreo con reemplazo.

   • Las instancias no seleccionadas forman los datos Out-of-Bag (OOB) para ese árbol.

2. Predicciones OOB:

   • Cada instancia es evaluada únicamente por los árboles donde no participó durante el entrenamiento.

   • Las predicciones finales de una instancia OOB son agregadas (por voto mayoritario o promedio) de todos los árboles donde fue OOB.

3. Cálculo del OOB Score:

   • Se compara la predicción agregada con las etiquetas reales para calcular una métrica global, como exactitud o AUC.

   • Este puntaje representa una estimación conservadora del rendimiento del modelo.

¿Por qué el OOB Score puede ser más bajo?

1. Menos Árboles Contribuyen:

   • El OOB Score usa solo los árboles donde la instancia fue OOB, lo que resulta en menos contribuciones para cada predicción, aumentando la varianza.

2. Evaluación Estricta:

   • Las instancias OOB son tratadas como datos “no vistos” por los árboles que las evalúan, lo que simula un conjunto de validación más estricto.

3. Generalización Conservadora:

   • Al no beneficiarse del conocimiento de todos los árboles, el OOB Score tiende a ser más bajo que el rendimiento en el conjunto de entrenamiento o incluso en un conjunto de prueba separado.

Notas:

• Evaluación Comparable: Aunque es más conservador, el OOB Score puede reflejar mejor cómo el modelo generalizará en datos no vistos.

• Sesgo en Datos Desbalanceados: En conjuntos con clases altamente desbalanceadas, el OOB Score puede subestimar el rendimiento real debido al sesgo hacia la clase mayoritaria.

• No Sustituye al Conjunto de Prueba: Si bien es útil como estimación inicial, el OOB Score no reemplaza la evaluación en un conjunto de prueba externo para medir la capacidad de generalización.

pd.DataFrame(clf_rf_full3.oob_decision_function_)

	0	1
0	0.142356	0.857644
1	0.066600	0.933400
2	0.282172	0.717828
3	0.253039	0.746961
4	0.107753	0.892247
...	...	...
30946	0.152940	0.847060
30947	0.142514	0.857486
30948	0.197629	0.802371
30949	0.081787	0.918213
30950	0.131068	0.868932

30951 rows × 2 columns

pd.DataFrame(clf_rf_full3.predict_proba(preprocessor.fit_transform(X_train)))

	0	1
0	0.143918	0.856082
1	0.066585	0.933415
2	0.280503	0.719497
3	0.258214	0.741786
4	0.107117	0.892883
...	...	...
30946	0.149155	0.850845
30947	0.143554	0.856446
30948	0.184611	0.815389
30949	0.098721	0.901279
30950	0.128493	0.871507

30951 rows × 2 columns

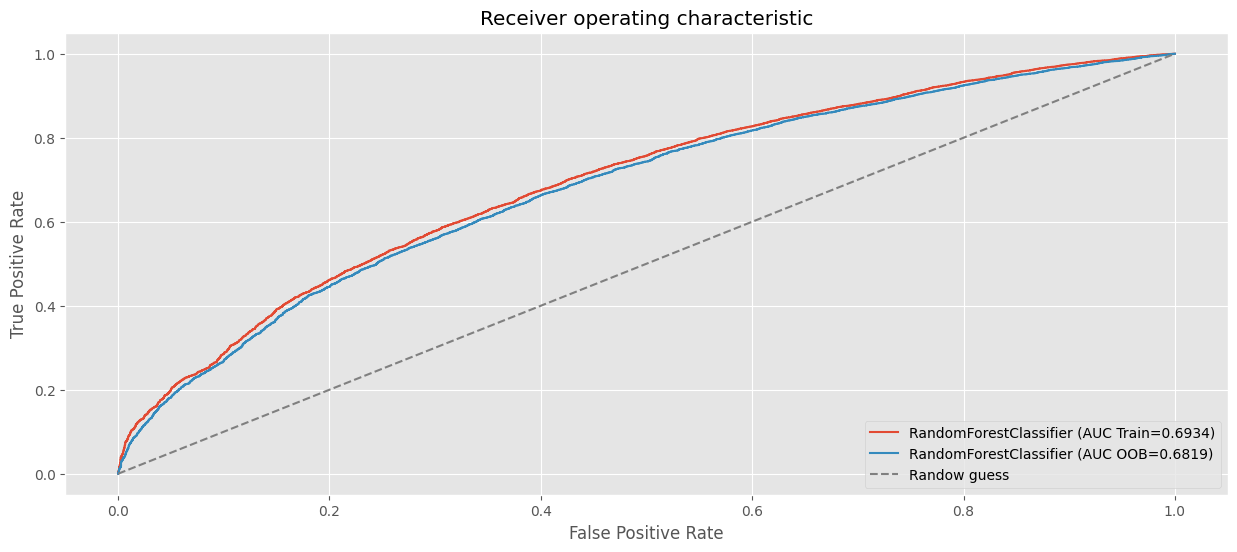
# AUC en train.
fpr, tpr, _ = roc_curve(y_train, clf_rf_full3.predict_proba(preprocessor.fit_transform(X_train))[:, 1])
plt.plot(fpr, tpr, label=f"RandomForestClassifier (AUC Train={auc(fpr, tpr):.4f})")

# AUC en test.
fpr, tpr, _ = roc_curve(y_train, clf_rf_full3.oob_decision_function_[:, 1])
plt.plot(fpr, tpr, label=f"RandomForestClassifier (AUC OOB={auc(fpr, tpr):.4f})")

plt.xlabel("False Positive Rate")
plt.ylabel("True Positive Rate")
plt.title("Receiver operating characteristic")
plt.plot((0,1), (0,1), ls="--", color="grey", label="Randow guess")
plt.legend(loc="lower right")
plt.show()

¿Cómo Elegir un Modelo de Clasificación?

La elección del modelo de clasificación depende de múltiples factores, siendo el rendimiento predictivo, como el AUC (Área bajo la curva), uno de los más importantes. Sin embargo, cuando el rendimiento de los modelos es similar, como en este caso, donde todos los modelos tienen resultados comparables, la decisión puede basarse en otros criterios como la varianza, la eficiencia computacional y el propósito del análisis.

Criterios para la Selección del Modelo

1. Finalidad del análisis

   • Si buscas un clasificador rápido y sencillo, los bosques aleatorios son una buena opción con configuraciones predeterminadas.

   • Si los datos tienen patrones bien entendidos, podrías usar la regresión logística con transformaciones manuales para capturar esos patrones.

2. Tamaño del conjunto de datos

• Con grandes volúmenes de datos:

  • Los bosques aleatorios y la regresión logística pueden volverse computacionalmente costosos debido a su complejidad.

  • Los bosques aleatorios son más adecuados cuando los datos son ricos y tienen interacciones complejas, aunque entrenarlos en grandes conjuntos de datos requiere más recursos.

3. Número de covariables

• Cuando el número de covariables es pequeño, tanto los bosques aleatorios como la regresión logística se desempeñan bien.

• A medida que aumenta el número de covariables:

  • Los bosques aleatorios capturan mejor las interacciones complejas.

  • La regresión logística podría requerir regularización para evitar sobreajuste.

Conclusiones

1. Diferencias entre modelos

   • Los bosques aleatorios son más lentos, pero capturan relaciones no lineales y patrones complejos en los datos.

   • La regresión logística, aunque más rápida y directa, puede no capturar interacciones no lineales sin agregar transformaciones explícitas.

2. Desempeño similar en el caso actual

   • Ambos modelos mostraron un desempeño similar debido al tamaño mediano del conjunto de datos y el número limitado de covariables.

   • La ausencia de sobreajuste sugiere que los datos son suficientes para un entrenamiento adecuado sin complejidad adicional.

3. Extensibilidad de los modelos

   • Bosques aleatorios:

     • Requieren ajuste fino de parámetros, como el número de árboles y la profundidad, para optimizar el desempeño según las características de los datos.

   • Regresión logística:

     • Puede beneficiarse de la regularización y es más adecuada para conjuntos de datos más pequeños y con menor complejidad.

4. La selección del modelo debe considerar el equilibrio entre:

   • Propósito del análisis: ¿Es una prueba rápida o un modelo optimizado para producción?

   • Eficiencia computacional: ¿Cuántos datos y covariables tiene el problema?

   • Capacidad del modelo para generalizar: ¿Los datos son lo suficientemente ricos para aprovechar modelos más complejos?

Hiperparámetros de Random Forest en Scikit-learn: Recomendaciones y Explicaciones

Un Random Forest es un modelo basado en árboles de decisión que utiliza el principio de ensembles para mejorar la precisión y reducir el sobreajuste. A continuación, se describen los hiperparámetros principales, incluidas las recomendaciones para optimizarlos:

• n_estimators

• Descripción: Número de árboles en el bosque.

• Recomendación:

  • Comienza con 100 y aumenta hasta que el rendimiento se estabilice (e.g., 200-500).

  • Más árboles ofrecen más estabilidad, pero aumentan el tiempo de cómputo.

• criterion

• Descripción: Función para medir la calidad de una división.

• Opciones:

  • gini: Índice de Gini (predeterminado). Mide la impureza de las particiones.

  • entropy: Ganancia de información. Basado en la reducción de entropía.

  • log_loss: Pérdida logarítmica (desde Scikit-learn 1.1). Permite obtener probabilidades calibradas.

• Recomendación:

  • Usa gini como punto de partida para la mayoría de los problemas.

  • Experimenta con entropy si prefieres divisiones basadas en entropía.

  • Usa log_loss si necesitas probabilidades calibradas o si el modelo debe ser compatible con métricas de puntuación probabilística (e.g., log-loss o Brier score).

• Nota: log_loss es útil para clasificación multiclase y puede ser más robusto cuando las clases están desbalanceadas.

• max_depth

• Descripción: Profundidad máxima de cada árbol.

• Recomendación:

  • Usa valores entre 5 y 20 para evitar el sobreajuste.

  • Si no se especifica, los árboles crecen hasta que las hojas sean puras.

  • Limitar la profundidad es útil para datos ruidosos.

• min_samples_split

• Descripción: Número mínimo de muestras para dividir un nodo.

• Recomendación:

  • Valor predeterminado: 2.

  • Para evitar divisiones con pocas observaciones, utiliza valores más altos, como 0.01 del total de datos.

• min_samples_leaf

• Descripción: Mínimo de muestras en una hoja.

• Recomendación:

  • Valores pequeños (1-5) para datos grandes.

  • Valores más altos (10-50) en datos ruidosos para árboles más simples.

• max_features

• Descripción: Número máximo de características consideradas en cada división.

• Recomendación:

  • Clasificación: Usa "sqrt" (raíz cuadrada del total de variables).

  • Para alta dimensionalidad: Usa "log2" o valores pequeños.

  • Predeterminado (auto) funciona bien para la mayoría de los casos.

• bootstrap

• Descripción: Si usar muestreo con reemplazo.

• Recomendación:

  • Usa True (predeterminado) para conjuntos grandes.

  • Cambia a False para conjuntos de datos pequeños.

• class_weight

• Descripción: Pesos de las clases en problemas de clasificación.

• Recomendación:

  • Usa "balanced" si hay desbalance entre las clases.

  • Asigna pesos personalizados si tienes conocimiento previo sobre su importancia.