K-means clustering

K-means clustering#

Universidad Central#

Maestría en analítica de datos#

Métodos estadísticos para analítica de datos.#

Docente: Luis Andrés Campos Maldonado.#

import mglearn
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA
from sklearn.cluster import KMeans
from utils.plots_clustering import (
    cluster_biplot,
    elbow_plot,
    plot_silhouette,
    gap_statistic
)

plt.style.use("ggplot")
plt.rcParams["figure.figsize"] = (15,6)
url_base = "https://raw.githubusercontent.com/lacamposm/Metodos-Estadisticos/main/data/"

\(k\)-means clustering#

El k-means clustering es uno de los algoritmos de agrupamiento más simples y más utilizados. Es de los métodos no supervisado para dividir un conjunto de individuos (registros del Dataset) en un conjunto de \(k\) grupos (es decir, \(k\) clusters), donde \(k\) representa el número de grupos preestablecidos. Este algoritmo busca que los objetos dentro del mismo cluster sean lo más similares posibles (es decir, alta similitud intraclase), mientras que distintos clusters sean lo más diferente posible (es decir, baja similitud entre clases).

En el \(k\)-means clustering, cada grupo está representado por su centro (es decir, centroide) que corresponde a la media de puntos asignados al cluster.

Algoritmo de \(k\)-means.#

El primer paso cuando se usa el algoritmo es indicar el número \(k\) de clusters que se desean obtener. El algoritmo comienza seleccionando aleatoriamente \(k\) objetos del conjunto de datos para que sirvan como centroides iniciales de los cluster. Seguido, cada uno de los registros restantes se asigna a su centroide más cercano (asignación de cluster), donde más cercano se asigna por la distacia euclideana. Después del paso de asignación, el algoritmo calcula el nuevo centroide de cada cluster (actualización del centroide). Ahora que los centroides se han vuelto a calcular, para cada observación se verifican las distancias para determinar si podría estar más cerca a un clúster diferente. Todos los objetos se reasignan nuevamente utilizando el centroide actualizado del clúster. Los pasos de asignación de cluster y actualización del centroide se repiten iterativamente hasta que las asignaciones de clústeres dejan de cambiar (se logra la convergencia), es decir, los clusters formados en la iteración actual son los mismos que los obtenidos en la iteración anterior.

El algoritmo \(k\)-means se puede resumir de la siguiente manera:

  1. Especifique el número de cluster (\(k\)) que se crearán.

  2. Seleccione aleatoriamente \(k\) registros del conjunto de datos como centroides de los clusters iniciales.

  3. Asigna cada registro a su centroide más cercano, basado en alguna distancia.

  4. Para cada uno de los \(k\) clusters, se actualiza el centroide del cluster.

  5. Iterar los pasos 3 y 4 hasta que las asignaciones de los clusters dejen de cambiar o el número máximo de iteraciones se alcanza.

Se asume que entre los individuos se puede establecer una distancia euclidiana.

La idea básica detrás de \(k\)-means clustering consiste en definir grupos de modo que el total de la variación intra-cluster se minimize (conocida como inertia, within-cluster sum-of-squares criterion, o within-cluster variation).

El algoritmo estándar define la variación intra-cluster como la suma de las distancias al cuadrado (euclidiana) al centroide y los elementos del cluster:

\[W(C_k) = \sum_{x_i \in C_{k}}||x_i -\mu_k||^2\]

• \(x_i\) es un registro que pertence al cluster \(C_k\).

• \(\mu_k\) es el valor promedio de los registros asignados al cluster \(C_k\)

Cada registro (\(x_i\)) se asigna a un cluster de tal forma que la suma de los cuadrados de la distancia de la observación a sus centroides \(\mu_k\) sea mínimo.

Definimos la inercia o within-cluster sum-of-squares como sigue:

\[WCSS =\sum_{n=1}^{k} W(C_n)= \sum_{n=1}^{k} \sum_{x_i \in C_{n}}||x_i -\mu_n||^2\]

El algoritmo \(k\)-means tiene como objetivo elegir centroides que minimicen la inercia. Esto mide la compacidad (es decir goodness) del agrupamiento, se desea que sea lo mas baja posible.

mglearn.plots.plot_kmeans_algorithm()
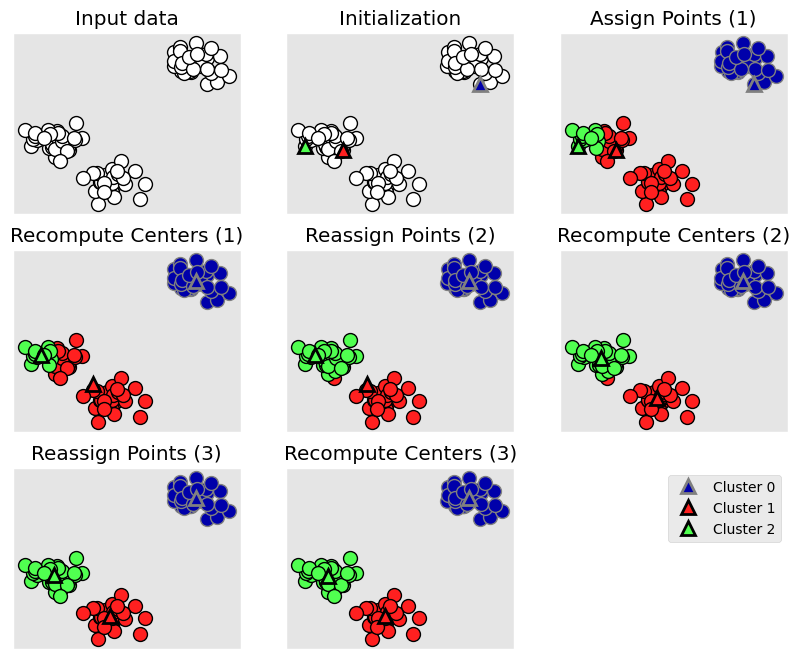
../_images/a37a09ae4af1069de8e21df09b5a64e8d0e94962c34e50292e0646365f226740.png

Método \(k\)-means#

Vamos a hacer uso de sklearn.cluster.KMeans para realizar el \(k\)-means clustering.

Ejemplo 1.#

df_usarrests = pd.read_csv(url_base + "USArrests.csv", index_col=0)
df_usarrests.head()
Murder Assault UrbanPop Rape
Alabama 13.2 236 58 21.2
Alaska 10.0 263 48 44.5
Arizona 8.1 294 80 31.0
Arkansas 8.8 190 50 19.5
California 9.0 276 91 40.6 
# Escalamos la información.
scaled_data = StandardScaler().fit_transform(df_usarrests)
pd.DataFrame(scaled_data, index=df_usarrests.index)
0 1 2 3
Alabama 1.255179 0.790787 -0.526195 -0.003451
Alaska 0.513019 1.118060 -1.224067 2.509424
Arizona 0.072361 1.493817 1.009122 1.053466
Arkansas 0.234708 0.233212 -1.084492 -0.186794
California 0.281093 1.275635 1.776781 2.088814
Colorado 0.025976 0.402909 0.869548 1.883901
Connecticut -1.040880 -0.736484 0.799761 -1.092723
Delaware -0.437875 0.815030 0.450825 -0.585834
Florida 1.765415 1.990786 1.009122 1.150530
Georgia 2.229265 0.487757 -0.386621 0.492653
Hawaii -0.577030 -1.512241 1.218484 -0.111300
Idaho -1.203228 -0.615272 -0.805344 -0.758392
Illinois 0.605789 0.948363 1.218484 0.298525
Indiana -0.136372 -0.700121 -0.037685 -0.025021
Iowa -1.295998 -1.391029 -0.595982 -1.071153
Kansas -0.414682 -0.675878 0.032102 -0.348567
Kentucky 0.443441 -0.748605 -0.944918 -0.531910
Louisiana 1.765415 0.948363 0.032102 0.104398
Maine -1.319191 -1.063757 -1.014705 -1.448624
Maryland 0.814521 1.566544 0.101889 0.708350
Massachusetts -0.785763 -0.263757 1.358058 -0.531910
Michigan 1.000062 1.021090 0.590399 1.495646
Minnesota -1.180036 -1.197090 0.032102 -0.682898
Mississippi 1.927762 1.069575 -1.503215 -0.445631
Missouri 0.281093 0.087757 0.311251 0.751490
Montana -0.414682 -0.748605 -0.875131 -0.521125
Nebraska -0.808955 -0.833454 -0.247047 -0.510340
Nevada 1.023254 0.984726 1.078909 2.671197
New Hampshire -1.319191 -1.378908 -0.665769 -1.265281
New Jersey -0.089987 -0.142545 1.637207 -0.262288
New Mexico 0.837714 1.384726 0.311251 1.172100
New York 0.768136 1.008969 1.427845 0.525008
North Carolina 1.208794 2.015028 -1.433428 -0.553480
North Dakota -1.620693 -1.524362 -1.503215 -1.502548
Ohio -0.113180 -0.615272 0.660186 0.018119
Oklahoma -0.275527 -0.239515 0.171676 -0.132870
Oregon -0.669800 -0.142545 0.101889 0.870123
Pennsylvania -0.345105 -0.784969 0.450825 -0.682898
Rhode Island -1.017688 0.039273 1.497632 -1.394700
South Carolina 1.533490 1.311999 -1.224067 0.136752
South Dakota -0.924918 -1.027393 -1.433428 -0.909380
Tennessee 1.255179 0.208970 -0.456408 0.611287
Texas 1.139217 0.366545 1.009122 0.460298
Utah -1.064073 -0.615272 1.009122 0.179892
Vermont -1.295998 -1.487999 -2.340661 -1.081938
Virginia 0.165131 -0.178909 -0.177259 -0.057376
Washington -0.878533 -0.312242 0.520612 0.535792
West Virginia -0.484260 -1.087999 -1.852151 -1.286851
Wisconsin -1.203228 -1.427393 0.032102 -1.125078
Wyoming -0.229142 -0.118303 -0.386621 -0.607404 
n = 2
kmeans = KMeans(
    n_clusters=n,       # Número de clusters
    random_state=0      # Semilla aleatoria.
)                                  

kmeans.fit(scaled_data) # Ajustamos el modelo.

KMeans(n_clusters=2, random_state=0)
In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.
# Atributos.
print(kmeans.inertia_)
print(kmeans.cluster_centers_)

104.96163315756871
[[ 1.01513667  1.02412028  0.19959126  0.85556386]
 [-0.67675778 -0.68274685 -0.13306084 -0.57037591]]

centroides = pd.DataFrame(kmeans.cluster_centers_, columns=df_usarrests.columns, index=[f"centroide_cluster_{i}" for i in range(n)])
centroides
Murder Assault UrbanPop Rape
centroide_cluster_0 1.015137 1.024120 0.199591 0.855564
centroide_cluster_1 -0.676758 -0.682747 -0.133061 -0.570376 
## Plot centroides.
temp = centroides.iloc[0:4,0:5]
temp.index = ["cluster0","cluster1"]
X_axis, a = np.arange(len(temp.columns)), np.flip(np.arange(-0.1,0.1,0.1))
##
for i,index in enumerate(temp.index):
  plt.bar(X_axis -1*a[i], temp.loc[index],width=0.1, label = index)
plt.xticks(X_axis,temp.T.index)
plt.xlabel("\nFeatures",)
plt.ylabel(" ",)
plt.title("Plot centroides")
plt.legend()
plt.show()
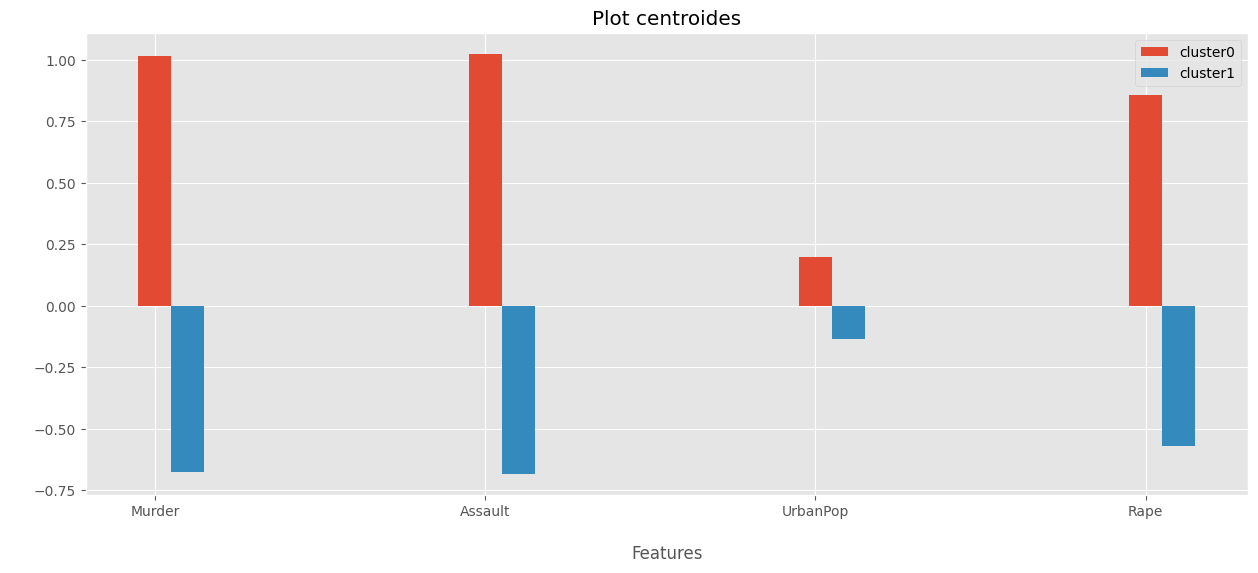
../_images/0255654d627ec6ba043c120464c1d06dde21a0065b5ab8e8baa34eb87764a521.png 
# Cluster de cada instancia
print(kmeans.labels_)

[0 0 0 1 0 0 1 1 0 0 1 1 0 1 1 1 1 0 1 0 1 0 1 0 0 1 1 0 1 1 0 0 0 1 1 1 1
 1 1 0 1 0 0 1 1 1 1 1 1 1]

df_cluster = df_usarrests.copy()
df_cluster["cluster"] = kmeans.labels_
df_cluster
Murder Assault UrbanPop Rape cluster
Alabama 13.2 236 58 21.2 0
Alaska 10.0 263 48 44.5 0
Arizona 8.1 294 80 31.0 0
Arkansas 8.8 190 50 19.5 1
California 9.0 276 91 40.6 0
Colorado 7.9 204 78 38.7 0
Connecticut 3.3 110 77 11.1 1
Delaware 5.9 238 72 15.8 1
Florida 15.4 335 80 31.9 0
Georgia 17.4 211 60 25.8 0
Hawaii 5.3 46 83 20.2 1
Idaho 2.6 120 54 14.2 1
Illinois 10.4 249 83 24.0 0
Indiana 7.2 113 65 21.0 1
Iowa 2.2 56 57 11.3 1
Kansas 6.0 115 66 18.0 1
Kentucky 9.7 109 52 16.3 1
Louisiana 15.4 249 66 22.2 0
Maine 2.1 83 51 7.8 1
Maryland 11.3 300 67 27.8 0
Massachusetts 4.4 149 85 16.3 1
Michigan 12.1 255 74 35.1 0
Minnesota 2.7 72 66 14.9 1
Mississippi 16.1 259 44 17.1 0
Missouri 9.0 178 70 28.2 0
Montana 6.0 109 53 16.4 1
Nebraska 4.3 102 62 16.5 1
Nevada 12.2 252 81 46.0 0
New Hampshire 2.1 57 56 9.5 1
New Jersey 7.4 159 89 18.8 1
New Mexico 11.4 285 70 32.1 0
New York 11.1 254 86 26.1 0
North Carolina 13.0 337 45 16.1 0
North Dakota 0.8 45 44 7.3 1
Ohio 7.3 120 75 21.4 1
Oklahoma 6.6 151 68 20.0 1
Oregon 4.9 159 67 29.3 1
Pennsylvania 6.3 106 72 14.9 1
Rhode Island 3.4 174 87 8.3 1
South Carolina 14.4 279 48 22.5 0
South Dakota 3.8 86 45 12.8 1
Tennessee 13.2 188 59 26.9 0
Texas 12.7 201 80 25.5 0
Utah 3.2 120 80 22.9 1
Vermont 2.2 48 32 11.2 1
Virginia 8.5 156 63 20.7 1
Washington 4.0 145 73 26.2 1
West Virginia 5.7 81 39 9.3 1
Wisconsin 2.6 53 66 10.8 1
Wyoming 6.8 161 60 15.6 1 
df_cluster.groupby(by=["cluster"]).mean()
Murder Assault UrbanPop Rape
cluster
0 12.165 255.250000 68.400000 29.165000
1 4.870 114.433333 63.633333 15.943333 
# Con 4 clusters
n = 4
kmeans1 = KMeans(
    n_clusters=n,
    random_state=0
)

kmeans1.fit(scaled_data)  

KMeans(n_clusters=4, random_state=0)
In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.
print(kmeans1.inertia_)
print(kmeans1.cluster_centers_)

58.241584331343226
[[ 0.75759426  1.13128272  0.94567938  1.22798509]
 [-0.44878894 -0.35858791  0.56576856 -0.20455729]
 [-0.97130281 -1.11783581 -0.93954982 -0.97657842]
 [ 1.32475684  0.90930557 -0.86737678  0.29612861]]

# Metodo predict en K-means
df_to_predict = pd.DataFrame(scaled_data, index=[f"new_instance_{i+1}" for i in range(len(scaled_data))])
sample = df_to_predict.sample(5)
display(sample)
kmeans.predict(sample)
0 1 2 3
new_instance_29 -1.319191 -1.378908 -0.665769 -1.265281
new_instance_22 1.000062 1.021090 0.590399 1.495646
new_instance_6 0.025976 0.402909 0.869548 1.883901
new_instance_21 -0.785763 -0.263757 1.358058 -0.531910
new_instance_27 -0.808955 -0.833454 -0.247047 -0.510340 
array([1, 0, 0, 1, 1], dtype=int32)

# Distancia de las instancia al centroide de cada cluster.
temp = pd.DataFrame(
    kmeans.transform(scaled_data),
    columns=[f"distance_cluster_{i}" for i in range(kmeans.n_clusters)],
    index=df_usarrests.index
)
temp["assign_cluster"] = kmeans.predict(scaled_data)
temp["assign_cluster"] = temp["assign_cluster"].astype("string")
temp
distance_cluster_0 distance_cluster_1 assign_cluster
Alabama 1.173345 2.525795 0
Alaska 2.241206 3.915857 0
Arizona 1.343111 3.039746 0
Arkansas 1.992482 1.649881 1
California 2.147210 3.933386 0
Colorado 1.694303 2.949777 0
Connecticut 3.388652 1.130697 1
Delaware 2.072609 1.625288 1
Florida 1.496565 4.168703 0
Georgia 1.495708 3.318037 0
Hawaii 3.307732 1.653913 1
Idaho 3.350149 0.876948 1
Illinois 1.233588 2.624330 0
Indiana 2.265107 0.773839 1
Iowa 3.939475 1.161980 1
Kansas 2.532264 0.381063 1
Kentucky 2.589281 1.385559 1
Louisiana 1.077478 3.017834 0
Maine 4.073342 1.451380 1
Maryland 0.604721 2.995591 0
Massachusetts 2.858145 1.553174 1
Michigan 0.750115 3.241392 0
Minnesota 3.485322 0.746845 1
Mississippi 2.329723 3.427396 0
Missouri 1.199539 1.859004 0
Montana 2.870059 0.791274 1
Nebraska 2.973730 0.238298 1
Nevada 2.017757 4.200854 0
New Hampshire 4.058382 1.289974 1
New Jersey 2.428732 1.965930 1
New Mexico 0.523620 3.130767 0
New York 1.295806 2.930173 0
North Carolina 2.381503 3.539002 0
North Dakota 4.680022 2.084610 1
Ohio 2.207752 1.139184 1
Oklahoma 2.059215 0.801072 1
Oregon 2.051799 1.556312 1
Pennsylvania 2.748280 0.688496 1
Rhode Island 3.442513 1.994045 1
South Carolina 1.701486 3.248773 0
South Dakota 3.708679 1.409342 1
Tennessee 1.100953 2.455284 0
Texas 1.122219 2.601086 0
Utah 2.850016 1.421988 1
Vermont 4.675348 2.483361 1
Virginia 1.773489 1.108040 1
Washington 2.361600 1.352362 1
West Virginia 3.938125 1.915696 1
Wisconsin 3.857726 1.080112 1
Wyoming 2.310255 0.764605 1

¿Cuántos cluster debemos seleccionar?#

Determinar el número óptimo de clusters en un Dataset es un problema fundamental en el agrupamiento. En \(k\)-means se requiere especificar de antemano el número de clústeres \(k\) que se generarán.

Desafortunadamente no hay una respuesta definitiva a esta pregunta. El número óptimo de clusters es algo subjetivo y depende del método utilizado para medir similitudes y los parámetros utilizados para la partición.

Una solución simple y popular consiste en inspeccionar el dendrograma producido por el agrupamiento jerárquico para ver si sugiere un número particular de grupos, de igual forma este enfoque también es subjetivo.

Vamos a describir diferentes métodos para determinar el número óptimo de clusters para \(k\)-means. Estos métodos incluyen métodos directos y métodos de prueba estadísticos:

  1. Métodos directos: consiste en optimizar un criterio, como el WCSS o la silueta media. Los métodos se denominan elbow method y silhouette, respectivamente.

  2. Métodos estadísticos de contraste: consiste en comparar la evidencia contra la hipótesis nula. Un ejemplo es la estadística de GAP.

Método del codo.#

La idea básica detrás de los método \(k\)-means, es definir clusters tales que WCSS se minimiza. Recordemos que WCSS mide la compacidad del agrupamiento y queremos que sea lo más pequeño posible.

El método codo analiza el WCSS como una función del número de clusters. Se debe elegir una cantidad de clusers de tal forma que agregar otro cluster no mejore mucho el valor WCSS.

El número óptimo de clústeres se puede definir de la siguiente manera:

  1. Calcule el algoritmo de clustering \(k\)-means para diferentes valores de \(k\). Puede variar \(k\) de 1 a 10 grupos.

  2. Para cada \(k\), calcule WCSS.

  3. Trazar la curva de WCSS según el número de clusters \(k\).

  4. La ubicación de una curva (codo) en el plot generalmente se considera como un indicador del número adecuado de clusters.

Tenga en cuenta que el método del codo a veces es ambiguo.

elbow_plot(df_usarrests, n=10, scaled_data=False)

Según lo observado, ¿cuántos cluster usted considera que se deben formar?

Coeficiente de silhouette#

El coeficiente de silueta mide qué tan bien se agrupa una observación y estima la distancia promedio entre clusters. El plot de silueta muestra una medida de qué tan cerca está cada punto en un cluster de los puntos en los clusters vecinos.

Para cada observación \(i\), el ancho de la silueta \(s_i\) se calcula de la siguiente manera:

  1. Para cada observación \(i\), calculamos la disimilitud (distancia) promedio \(a_i\) entre \(i\) y todos los otros puntos del clúster al que pertenezca \(i\).

  2. Para todos los demás clusters \(C\), a los que no pertenezca \(i\), calcule el promedio de disimilitud \(d(i,C)\) de \(i\) con todos los puntos de \(C\). La menor de estas \(d(i,C)\) se define como \(b_i = min_C\ d(i,C)\). El valor de \(b_i\) puede verse como la disimilitud promedio entre \(i\) y su cluster “vecino”, es decir, el más cercano al que no pertenece.

  3. Finalmente, el ancho de la silueta de la observación \(i\) se define mediante la fórmula: $\(S_i = \frac{(b_i - a_i)}{max(a_i, b_i)}\)$

El ancho de la silueta se puede interpretar de la siguiente manera:

  • Las observaciones con un \(S_i\) grande (casi 1) están muy bien agrupadas.

  • Un \(S_i\) pequeño (alrededor de 0) significa que la observación se encuentra entre dos grupos.

  • Las observaciones con un \(S_i\) negativo probablemente estén ubicadas en el cluster incorrecto.

El algoritmo es similar al método del codo y se puede calcular de la siguiente manera:

  1. Calcule el algoritmo \(k\)-means para diferentes valores de \(k\). Por ejemplo, variando \(k\) de 1 a 10 grupos.

  2. Para cada \(k\), calcule la silueta promedio de las observaciones.

  3. Trazar el plot según el número de clusters y la silueta promedio.

  4. La ubicación del máximo se considera como el número apropiado de clusters.

plot_silhouette(df_usarrests, n=10, scaled_data=False)

El criterio estricto, nos diría que la mejor elección son 2 clusters.

GAP Statistic#

Este estadístico compara, para diferentes valores de \(k\), el WCSS observado frente al valor esperado acorde a una distribución uniforme de referencia. La estimación del número óptimo de clusters es el valor \(k\) con el que se consigue maximizar el estadístico GAP, es decir, encuentra el valor de \(k\) con el que se consigue una estructura de clusters lo más alejada posible de una distribución uniforme aleatoria. Este método puede aplicarse a cualquier tipo de clustering.

El algoritmo del gap statistic method es el siguiente:

  1. Hacer clustering de los datos para un rango de valores de \(k\) y calcular para cada uno el valor de WCSS.

  2. Simular \(B\) sets de datos de referencia, todos ellos con una distribución aleatoria uniforme. Aplicar clustering a cada uno de los sets con el mismo rango de valores \(k\) empleado en los datos originales, calculando en cada caso \(W_{kb}\). Se recomienda emplear valores de \(B=500\).

  3. Calcular el estadístico GAP para cada valor de \(k\) como la desviación de la varianza observada WCSS respecto del valor esperado acorde a la distribución de referencia \(W_{kb}\).

\[GAP(k)=\frac{1}{B}\sum_{b=1}^{B}log(W_{kb})−log(WCSS)\]

La estimación de los clústeres óptimos será el valor que maximice la estadística de GAP.

gap_statistic(df_usarrests, nrefs=40, max_clusters=10, scaled_data=False, random_state=42)

En este caso el caso el número de clusters a selecionar debe ser de 4 clusters.

Visualización de los cluster.#

Vamos a hacer uso de PCA para lograr visualizar los cluster.

pca = PCA(n_components=0.90)
pca_transform = pca.fit_transform(scaled_data)
print("Reduccion a", pca.n_components_, "dimensiones")

kmeans = KMeans(n_clusters=2, random_state=42)
kmeans.fit(pca_transform)

Reduccion a 3 dimensiones

KMeans(n_clusters=2, random_state=42)
In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.
df_with_pca = pd.DataFrame(pca_transform, index=df_usarrests.index, columns=[f"PC{i+1}" for i in range(pca.n_components_)])
df_with_pca["cluster"] = kmeans.labels_
df_with_pca
PC1 PC2 PC3 cluster
Alabama 0.985566 -1.133392 -0.444269 1
Alaska 1.950138 -1.073213 2.040003 1
Arizona 1.763164 0.745957 0.054781 1
Arkansas -0.141420 -1.119797 0.114574 0
California 2.523980 1.542934 0.598557 1
Colorado 1.514563 0.987555 1.095007 1
Connecticut -1.358647 1.088928 -0.643258 0
Delaware 0.047709 0.325359 -0.718633 0
Florida 3.013042 -0.039229 -0.576829 1
Georgia 1.639283 -1.278942 -0.342460 1
Hawaii -0.912657 1.570460 0.050782 0
Idaho -1.639800 -0.210973 0.259801 0
Illinois 1.378911 0.681841 -0.677496 1
Indiana -0.505461 0.151563 0.228055 0
Iowa -2.253646 0.104054 0.164564 0
Kansas -0.796881 0.270165 0.025553 0
Kentucky -0.750859 -0.958440 -0.028369 0
Louisiana 1.564818 -0.871055 -0.783480 1
Maine -2.396829 -0.376392 -0.065682 0
Maryland 1.763369 -0.427655 -0.157250 1
Massachusetts -0.486166 1.474496 -0.609497 0
Michigan 2.108441 0.155397 0.384869 1
Minnesota -1.692682 0.632261 0.153070 0
Mississippi 0.996494 -2.393796 -0.740808 1
Missouri 0.696787 0.263355 0.377444 1
Montana -1.185452 -0.536874 0.246889 0
Nebraska -1.265637 0.193954 0.175574 0
Nevada 2.874395 0.775600 1.163380 1
New Hampshire -2.383915 0.018082 0.036855 0
New Jersey 0.181566 1.449506 -0.764454 0
New Mexico 1.980024 -0.142849 0.183692 1
New York 1.682577 0.823184 -0.643075 1
North Carolina 1.123379 -2.228003 -0.863572 1
North Dakota -2.992226 -0.599119 0.301277 0
Ohio -0.225965 0.742238 -0.031139 0
Oklahoma -0.311783 0.287854 -0.015310 0
Oregon 0.059122 0.541411 0.939833 0
Pennsylvania -0.888416 0.571100 -0.400629 0
Rhode Island -0.863772 1.491978 -1.369946 0
South Carolina 1.320724 -1.933405 -0.300538 1
South Dakota -1.987775 -0.823343 0.389293 0
Tennessee 0.999742 -0.860251 0.188083 1
Texas 1.355138 0.412481 -0.492069 1
Utah -0.550565 1.471505 0.293728 0
Vermont -2.801412 -1.402288 0.841263 0
Virginia -0.096335 -0.199735 0.011713 0
Washington -0.216903 0.970124 0.624871 0
West Virginia -2.108585 -1.424847 0.104775 0
Wisconsin -2.079714 0.611269 -0.138865 0
Wyoming -0.629427 -0.321013 -0.240659 0 
# Plot con 2 clusters.
cluster_biplot(pca, df_usarrests, kmeans.labels_, size_text=5)

# Consideremos 4 clusters.
kmeans1 = KMeans(n_clusters=4,random_state=0).fit(pca_transform); kmeans1

KMeans(n_clusters=4, random_state=0)
In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.
# Plot con 4 clusters.
cluster_biplot(pca, df_usarrests, kmeans1.labels_, size_text=6)

# Caso 2 clusters
df_clusters2 = df_usarrests.copy()
df_clusters2["cluster"] = kmeans.labels_
df_clusters2["cluster"] = df_clusters2["cluster"].astype("category")
df_clusters2.head()
Murder Assault UrbanPop Rape cluster
Alabama 13.2 236 58 21.2 1
Alaska 10.0 263 48 44.5 1
Arizona 8.1 294 80 31.0 1
Arkansas 8.8 190 50 19.5 0
California 9.0 276 91 40.6 1 
# Box-plots
fig, axes = plt.subplots(2,2, sharex=True)

sns.boxplot(data=df_clusters2, x = "cluster", y = "Murder", ax=axes[0,0])
sns.boxplot(data=df_clusters2, x = "cluster", y = "Assault", ax=axes[0,1])
sns.boxplot(data=df_clusters2, x = "cluster", y = "UrbanPop", ax=axes[1,0])
sns.boxplot(data=df_clusters2, x = "cluster", y = "Rape", ax=axes[1,1])
fig.suptitle("Boxplot para features con 2 Clusters", fontsize=14, fontweight="bold",)
plt.show()
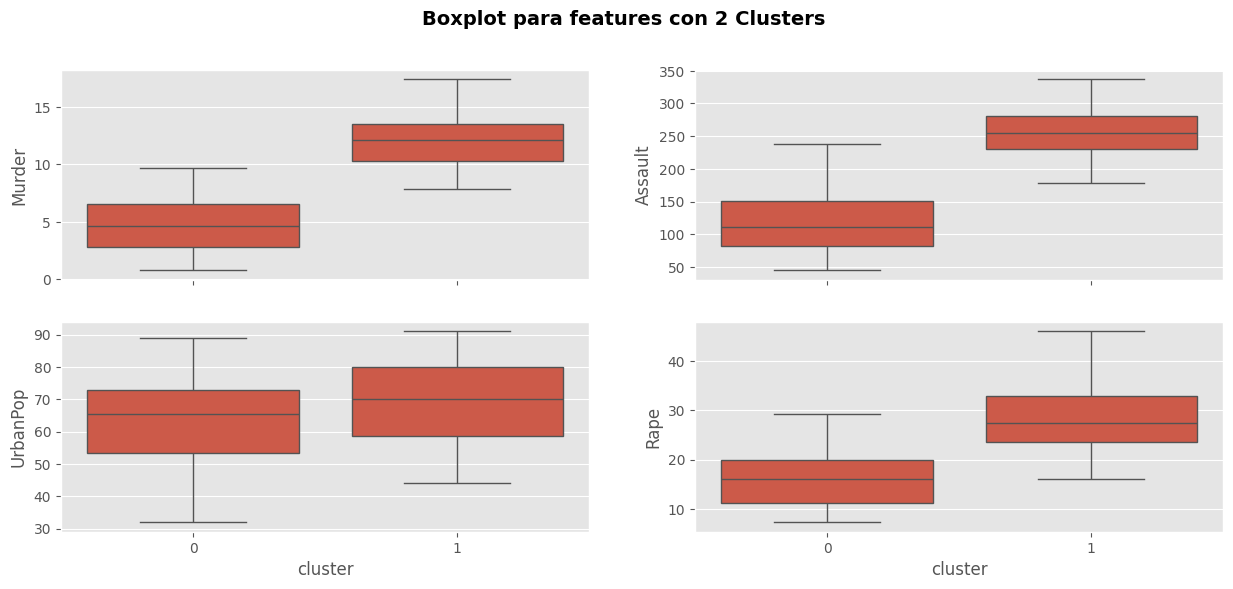
../_images/df20434e426eeadb9e6f862161bfcf9a4b43b454f077b74d9f868d2b512b85d2.png

Comentarios:

  1. El cluster 1 tiene una alta tasa delictiva y predomina la población urbana.

  2. El cluster 0 tiene tasas bajas de delitos y una menor tasa que el cluster 1 de población urbana.

Note que la solución en este caso es bastante simple, pues solo está teniendo en consideración las tasas de crimenes altos con “población urbana” y tasa de crimenes bajos con “población rural”. Esta solución parece ser buena, pues logra identificar los estados que tienen alto y bajo crimen.

n = 4
kmeans = KMeans(n_clusters=n,                  # Número de clusters
                random_state=0)                # Semilla aleatoria.
kmeans.fit(pca_transform)                        # Ajustamos el modelo.

KMeans(n_clusters=4, random_state=0)
In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.
# Caso 4 clusters
df_clusters4 = df_usarrests.copy()
df_clusters4["cluster"] = kmeans.labels_
df_clusters4.head()
Murder Assault UrbanPop Rape cluster
Alabama 13.2 236 58 21.2 3
Alaska 10.0 263 48 44.5 0
Arizona 8.1 294 80 31.0 0
Arkansas 8.8 190 50 19.5 3
California 9.0 276 91 40.6 0 
# Box-plots
fig, axes = plt.subplots(2,2, sharex=True)
#
sns.boxplot(data=df_clusters4, x = "cluster", y = "Murder", ax = axes[0,0])
sns.boxplot(data=df_clusters4, x = "cluster", y = "Assault", ax = axes[0,1])
sns.boxplot(data=df_clusters4, x = "cluster", y = "UrbanPop", ax = axes[1,0])
sns.boxplot(data=df_clusters4, x = "cluster", y = "Rape", ax = axes[1,1])
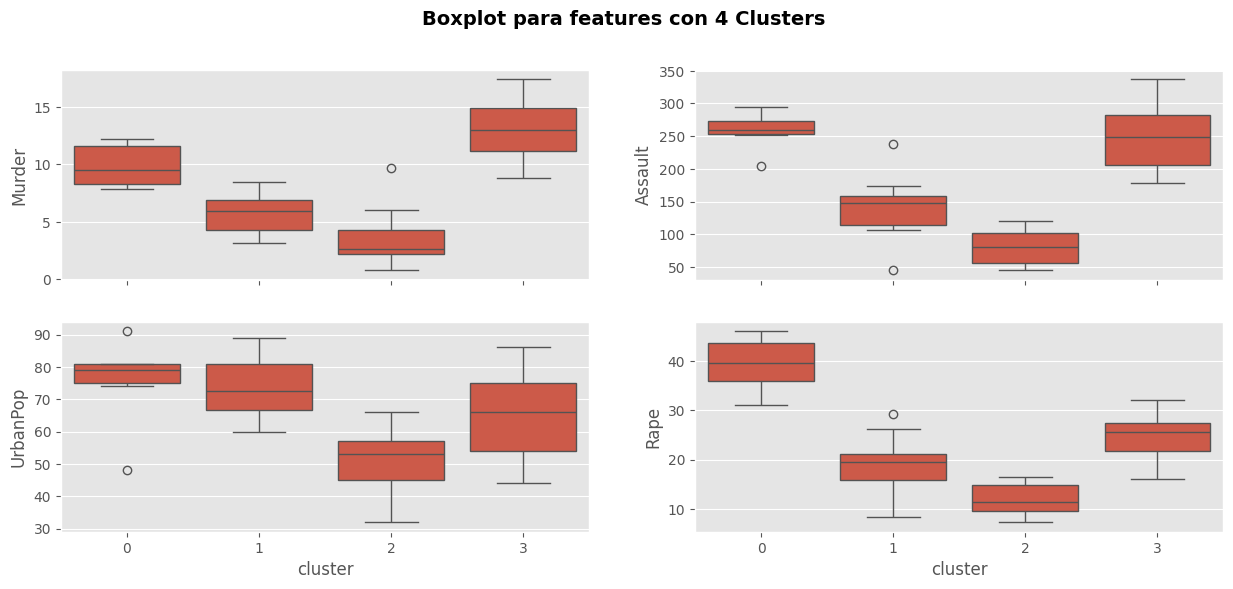
fig.suptitle("Boxplot para features con 4 Clusters", fontsize=14, fontweight="bold",)
plt.show()
../_images/bb76fbaca99ba591a917f7ae2f90b99c1083801b06779effab0ead50626040fd.png 
# Box-plots
fig, axes = plt.subplots(2,2, sharex=True)
#
sns.boxplot(data=df_clusters4, x="cluster", y="Murder", ax=axes[0,0])
sns.boxplot(data=df_clusters4, x="cluster", y="Assault", ax=axes[0,1])
sns.boxplot(data=df_clusters4, x="cluster", y="UrbanPop", ax=axes[1,0])
sns.boxplot(data=df_clusters4, x="cluster", y="Rape", ax=axes[1,1])
fig.suptitle("Boxplot para features con 4 Clusters", fontsize=14, fontweight="bold",)
plt.show()
../_images/bb76fbaca99ba591a917f7ae2f90b99c1083801b06779effab0ead50626040fd.png

Comentarios:

  1. El cluster 3 tiene alto el índice de asesinatos. El cluster 2 tiene un menor índice de asesinatos.

  2. Assault y Murder tiene un comportamiento similar para los clusters.

  3. Note que el cluster 1 tiene una tasa más alta de asaltos que el cluster 3. A su vez el cluster 3 tiene más asesinatos. Los clusters 0 y 2 tiene un compartamiento similar en ambas features (Assault y Murder).

  4. En cuanto a UrbanPop el cluster 0 y tienen cluster 1 tiene las tasas más altas. Por su supuesto los individuos en los cluster 2 y 3 tiene una tasa baja de población urbana.

Note que podemos caracterizar los cluster así:

  • Cluster 0: Baja tasa de delitos, y una alta tasa de población urbana.

  • Cluster 1. Alta tasa en todas las features.

  • Cluster 2. Baja tasa en todas las features.

  • Cluster 3. Alta tasa de Murder y Assault con baja tasa de población urbana y violaciones.

Esta solución parece ser buena, en este caso podemos pensar en una segmentación basados en la feature UrbanPop, note que acá tenemos más información que con 2 clusters.

Referencias:#

  1. Análisis estadístico de datos multivariados. Díaz L & Morales M. Editorial: Publicaciones Facultad de ciencias. UNAL.

  2. Multivariate Analysis I. Kassambara A. Disponible en: http://www.sthda.com/english/

  3. Selecting the number of clusters with silhouette analysis on KMeans clustering by sklearn